Trygonometria Tyrf: Dla jakich wartości parametru k równanie 3cosx+cos2x=k ma rozwiązanie? Przekształcam to na równanie kwadratowe i mam problem z warunkami Wiem że Delta musi być większa od zera, ale co dalej? Mógłby ktoś mi to ładnie objaśnić? z² + 3z − 1 −k = 0

piotr: to jest typ równania kiedy niewieadoma k pozostaje po prawej stronie a lewą strone musisz przekształcić zaraz Ci to rozpisze

piotr: 3cosx+2cos²x−1=k 2cos²x+3cosx−1=k Niech cosx=t, t ∊<−1,1> 2t²+3t−1=k Lewą częśc narysuj a niewiadoma 'k' to stała (prosta) która przecina wykres

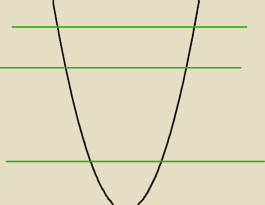
piotr: coś takiego tylko pamiętaj o dziedzinie

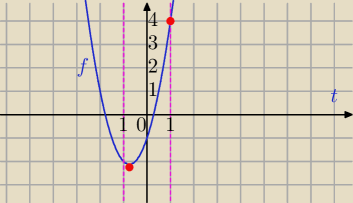
Mila: 1) Wyznaczymy zbiór wartości funkcji: f(x)=3cosx+cos(2x)⇔ f(x)=3cosx+2cos²x−1 f(x)=2cos²x+3cos−1 Podstawienie: cosx=t, |t|≤1 f(t)=2t²+3t−1

	−3		3
tw=		∊<−1,1>⇔najmniejsza wartość f(t) osiąga dla t=−
	4		4

	3		17
f(−		)=−
	4		8

Największa na końcu przedziału f(−1)=2−3−1=−2 f(1)=2+3−1=4 − największa wartość f(t) w przedziale <−1,1>. odp.

	17
równanie posiada rozwiązanie dla k∊<−		,4>
	8

Tyrf: Bardzo dziękuję