Na boku BC trójkata ABC wybrano taki punkt D Hohlik: Nie umiałem tam się dalej odwołać, więc zakładam nowy wątek. W tym zadaniu: https://matematykaszkolna.pl/forum/269297.html Wklejam treść: Na boku BC trójkata ABC wybrano taki punkt D, że pole trójkąta ADC jest równe trzeciej części pola trójkata ABC. a)Wyznacz stosunek długości odcinków BD i DC. b)Oblicz tanges kąta CAD, jęsli trójkąt ABC jest równoboczny. potrafię podpunkt a) bez problemu, lecz nie mam pojęcia jak zrobić b)... Przeszukałem już chyba wszędzie i nigdzie nie potrafię tego znaleźć. Proszę o pomoc :C

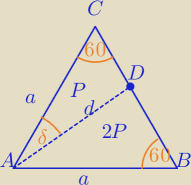
Mila: P_ΔABC=3P a)

BD		2
	=
DC		1

	1
|CD|=		a
	3

Z tw. cosinusów w ΔADC

	1		1
d2=a2+(		a)2−2*a*		a*cos60o
	3		3

	1		a2
d2=a2+		a2−
	9		3

	7		√7
d2=		a2, ⇔d=		a
	9		3

	1
PΔCAD=		*a*d*sinδ
	2

	1		a2√3
PΔCAD=		*
	3		4

−−−−−−−−−−−−−−−−−⇔

a2√3		1		√7
	=		*a*		a*sinδ
12		2		3

	√3
sinδ=
	2√7

	√3
cos2δ=1−(		)2
	2√7

	5
cosδ=
	2√7

	sinδ		√3
tgδ=		=
	cosδ		5

Posprawdzaj rachunki

Hohlik: Ojej...że na to nie wpadłem. Wszystko pasuje, dzięki wielkie Mila!

Mila: Zgadza się odpowiedź?

Hohlik: Tak jest ! Masz może jeszcze zadania podobnego pokroju, bo mam z nimi często problemy, a chciałbym poćwiczyć przed maturką ?

Eta: 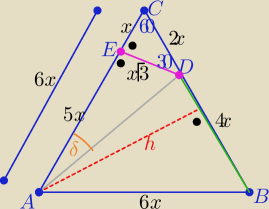2 sposób Z treści zadania uwzględniając pola (jak podała Mila

|BD|		4x
	=		=2 to |AC|=6x , x>0
|CD|		2x

w trójkącie DEC "ekierka" o kątach 30^o,60^o,90^o |CD|=2x, |CE|=x, |DE|=x√3 to |AE|= 6x−x=5x

	x√3		√3
tgδ=		=
	5x		5

Hohlik: Sprytnie Eta, dzięki wielkie

Eta:

Jack: pytalem oto samo jakis czas temu...2 razy pitagoras i po sprawie ;x