Oblicz kąt nachylenia przekątnej graniastosłupa. kama0966: Krawędź podstawy ABCD graniastosłupa prawidłowego czworokątnego ABCDA'B'C'D' jest równa 12 Na krawędzi bocznej DD' obrano punkt P taki ,że |PD'|=13.Graniastosłup ten przecięto płaszczyzną zawierającą przekątną AC podstawy i przechodzącą przez punkt P. Pole tego przekroju jest równe 54 √2.Oblicz kąt nachylenia przekątnej tego graniastosłupa do podstawy ABCD. Wynik podaj w stopniach z dokładnością do 1 stopnia. Rozwiąże ktoś , wytłumaczy co robi , krok po kroku ?

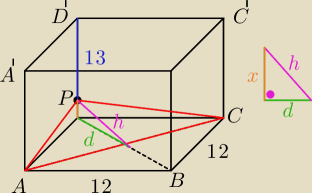
Jack: podstawa przekroju jest przekatna kwadratu czyli tutaj 12√2

	1
Pole przekroju =		* 12√2 * h = 6√2 * h
	2

z polecenia P = 54√2

	54
6√2 * h =54√2 −>>>h =		= 9
	6

	12√2
d to polowa przekatnej kwadratu czyli		= 6√2
	2

z pitagorasa x² = h² − d² = 9² − (6√2)² = 81 − 72 = 9 x = 3 zatem wysokosc graniastoslupa = 13 + 3 = 16 graniastoslup ma wymiary 12 X 12 X 16

kama0966: DZIĘKUJĘ BARDZO

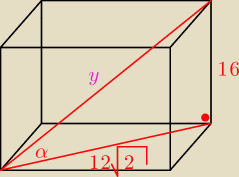
Jack: kat mozna wyznaczyc np. z tangensa

	16		16√2		8√2		2√3
tg α =		=		=		=
	12√2		12*2		12		3

albo z pitagorasa obliczamy dlugosc przekatnej y² = 16² + (12√2)² = 256 + 288 = 576 y = 24

	16		4		2
sin α =		=		=
	24		6		3

odczytaj z tablic...

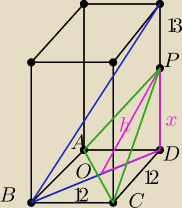
prosta: 1. Pole przekroju −−−> 12√2h=2*54√2 h=9 2. x²=h²−(6√2)² x²=81−72 x=3 3. H=16