Dowód w trapezie równoramiennym konwes97: W trapez równoramienny ABCD wpisano okrąg o środku O. Pokaż że średnia arytmetyczna długości podstaw ABCD jest równa √|OA|² + |OD|².

paymyove: Dany jest trójkąt ABC, w którym bok BC jest dwa razy dłuższy od boku AB, a kąt ABC jest dwa razy większy od kąta BAC. Pokaż, że |AC|² = 6|AB|²

konwes97 : wpisz głąbie własne pytanie

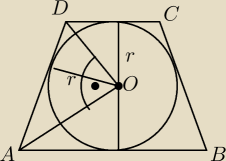
g: Kąt AOD jest prosty ze względu na podobieństwo par trójkątów. Jedna para ma wspólny bok OA, druga para OD.

	|AB|+|CD|		|AB|*r		|CD|*r
Pole trapezu =		*2r = |AD|*r +		+
	2		2		2

|AD| = √|OA|² + |OD|² itd.

konwes97 : dzięki wielkie