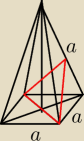
 Dany jest ostrosłup prawidłowy czworokątny, którego wszystkie krawędzie mają długość a.
Ostrosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i środek przeciwległej
do niej krawędzi bocznej. Ile jest równe pole otrzymanego przekroju?
Dlaczego jeśli wyliczam pole ze wzoru P=1/2 * a*c*sinβ to wynik wychodzi mi zły?
Przecież wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi, więc każdy kąt ma
60 stopni...
Dany jest ostrosłup prawidłowy czworokątny, którego wszystkie krawędzie mają długość a.
Ostrosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i środek przeciwległej
do niej krawędzi bocznej. Ile jest równe pole otrzymanego przekroju?
Dlaczego jeśli wyliczam pole ze wzoru P=1/2 * a*c*sinβ to wynik wychodzi mi zły?
Przecież wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi, więc każdy kąt ma
60 stopni...
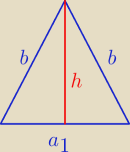 a1 = a√2
a1 = a√2
| √3 | ||
b = a | ||
| 2 |
| a√3 | ||
b= | . | |
| 2 |
| a√2 | a√3 | |||
h2 + ( | )2 = ( | )2 | ||
| 2 | 2 |
| 3 a2 | 2 a2 | a2 | ||||
h2 = | − | = | ||||
| 4 | 4 | 4 |
| a | ||
h = | ||
| 2 |
| a | a2 √2 | |||
P = 0,5 a√2* | = | |||
| 2 | 4 |
 Pitagorasa nie umiesz?
Pitagorasa nie umiesz?
 Mam jeszcze tylko pytanie, co jest złego w moim rozumowaniu jakie opisałam w pytaniu?
Mam jeszcze tylko pytanie, co jest złego w moim rozumowaniu jakie opisałam w pytaniu?