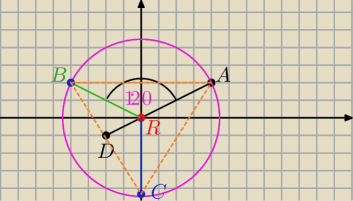
Planimetria? Jack: Punkt D(−2,−1) jest spodkiem wysokości opuszczonej z wierzchołka A(4,2) trójkąta równobocznego ABC. Wyznacz współrzędne pozostałych wierzchołków trójkąta Oznaczylem przez R jako srodek okregu opisanego na tym trojkacie. R(0,0) oraz gdzie mniej wiecej znajduja sie punkty B,C.

	√3
sin 120 = sin(180−60) =
	2

	√3
sin(−120) = − sin 120 = −
	2

	1
cos 120 = cos(−120) = −
	2

korzystajac ze wzoru na obrot punktu o kat wzgledem innego punktu. punkt B − obrot punktu A wzgledem punktu R o (120) stopni punkt C − obrot punktu A wzgledem punktu R o (− 120) stopni x_B = (x_A−x_R)*cosα − (y_A−y_R)*sinα+ x_R =

	1		√3
= 4*cos 120 − 2sin 120 + 0 = 4*(−		) − 2(		) = − 2 − √3
	2		2

y_B = (x_A−x_R)*sinα − (y_A−y_R)*cosα+y_R =

	1
= 4sin120 − 2cos120 + 0 = 2√3 − 2(−		) = 2√3 + 1
	2

B(−2−√3, 1+2√3) x_C = (x_A−x_R)*cosβ − (y_A−y_R)*sinβ+ x_R =

	1		√3
= 4*cos(−120) − 2sin(−120) + 0 = 4(−		) − 2(−		) = −2 + √3
	2		2

y_C = (x_A−x_R)*sinβ − (y_A−y_R)*cosβ+y_R =

	√3		1
= 4sin(−120) − 2cos(−120) + 0 = 4(−		) −2(−		) = −2√3 + 1
	2		2

C(−2+√3 , 1 − 2√3) ?

RObert: Robiłem to samo zadanie i ten wynik jest poprawny.

Metis: A bez obrotu punktu

Metis: A to z Tobą chyba robiłem to zadanie ?

Jack: bez obrotu to wektorowo, proste prostopadle itd...ale skoro wzor znam to nie moge korzystac z tego...nawet na maturze

Jack: to moge korzystac *

Mila: 1) równanie prostej AD 2) prosta BC⊥AD 3)S− środek okręgu opisanego na Δrównobocznym D=(−2,−1)→T_u^→⇒S(..,..)

	1
u→=		[6,3]=[2,1]
	3

S=(−2+2,−1+1)=(0,0) 3)Układ : równanie okręgu: x²+y²=|SA|² i równanie prostej BC

Jack: no ok, ale moge moim tak ? : D

Mila: Możesz, o ile dobrze zastosujesz wzory. Ja nie pamiętam i musiałabym wyprowadzić, a to więcej czasu zajmie niż tradycyjne sposoby.