Planimetria dowód Marian : W trójkąt prostokątny wpisano okrąg. Punkt styczności przeciwprostokątnej z okregiem dzieli ją na odcinki o długościach x i y. Wykaż, że pole trójkąta jest równe xy

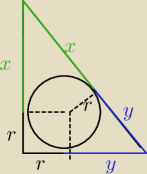
Qulka: (x+r)²+(y+r)²=(x+y)² x²+2xr+r²+y²+2yr=r²=x²+2xy+y² więc (x+y)r+r² = xy

	(x+r)(y+r)		xy+r(x+y)+r2		xy+xy
P=		=		=		= xy
	2		2		2

Marian : Dziękuję bardzo

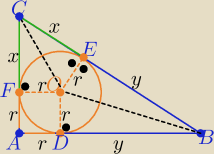
Eta: 2 sposób P(ABC)= P(ADOF) +P(DBEO)+P(ECFO) = r²+rx+ry = r²+r(x+y)=P 2P(ABC)=(x+r)(y+r)⇒2P=xy+r²+r(x+y) ⇒2P= xy+P ⇒ P=xy