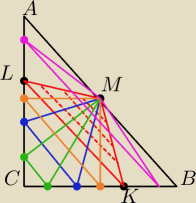
kwadratowa 6latek: W trojkacie ABC jest |AB|=2 |AC|=|BC| i kątACB=90 stopni W trojkat ABC wpisano trojkat LMK tak ze M jest srodkiem AB punk L należy do AC a punkt K należy do BC i KL||AB Zbadaj pole trojkata LMK jak funkcje dlugosci odcinka CL Sporzadz wykres Mamy tak Z treści zadania wynika ze trojkat ABC to trojkat prostokątny równoramienny w takim razie

	CB
sinα=
	AB

	√2
CB= sin		*2= √2
	2

CB=AC=√2 Wiec wynika z tego ze trojkat LMK będzie trójkątem równoramiennym a dla CL i CK trójkątem równobocznym |CL|∊(0,√2) Jeśli obliczymy wysokość trojkata ABC h²= (√2)²−1²= 1 wiec h=1 Ale chyba ta wysokość nam nic nie da .

6latek: Narysowalem kilka takich trojkatow żeby zobaczyć jak to będzie wygladac Jakas konkretna podpowiedz

wmboczek: wyraź pole jako różnicę pól dużego i 3 małych trójkątów

6latek: Pole dużego to P_d=1 Ale pozostałych nie wiem jak zrobić

wmboczek: x²/2, i dwa po 1/2sin45(√2−x)

6latek: Wiec tak Trojkaty KBM i LAM pole obliczone ze wzoru P=0,5sinαa*b gdzie a=√2−x i b=1 Trojkat CLK pole policzone ze wzoru P=0,5*a*h gdzie a i h=x Wobec tego pole trojkata LKM będzie wyrazac się wzorem

	x2
P=1−		−2*(0,5sin45*(√2−x)
	2

	1		1		√2
P=1−		x2−2(		*		(√2−x))
	2		2		2

Dokoncze te obliczenia sobie . Dziekuje Ci za pomoc