trygo Metis: Nierówność trygonometryczna: −2cos3x≥1 /:(−2)

	1
cos3x≤−
	2

	π
cos3x≤cos(−		)
	3

Czy do tego momentu jest ?

ZKS:

	π		1
cos(−		) ≠ −
	3		2

Metis:

	π
−cos3x≥cos(		)
	3

	π
cos(3x+π)≥cos(		)
	3

?

ZKS: Może być.

Metis: I teraz nie jestem pewny czy mogę zrobić przeskok do argumentów − nic nie stanie się ze znakiem nierówności? −−−−−−−−−−−−−−−−−−

	1
cos3x≤−
	2

	π
cos3x≤−cos(		)
	3

	π
cos3x≤cos(		+π)
	3

ZKS:

	π
Teraz już nie rozumiem zapisałeś cos(3x + π) ≥ cos(		), żeby znowu zamienić?
	3

mat: rozwiązujesz dla samego x, a potem dzielisz przez 3

Metis: No nie

Mila:

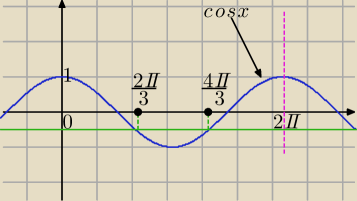
	1
cos(u)=		podajemy serię rozwiązań
	2

	π		π
u=		+2kπ lub u=−		+2kπ
	3		3

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1
cos(u)=−		⇔
	2

	π		π
u=		+π+2kπ lub u=−		+π+2kπ
	3		3

	4π		2π
u=		+2kπ lub u=		+2kπ
	3		3

	1
cos(3x)≤−
	2

Teraz odczytaj i napisz odpowiedź.

ZKS:

ZKS:

	1
Ty Metis zrób dla cos(3x + π) ≥		.
	2

mat: czyli dla samego x masz X należy (2π/3 +2kπ ; 4π/3 +2kπ) i teraz dzielisz to przez 3 czyli ostatecznie X (2π/9 +2/3kπ ; 4π/9 +2/3kπ), ja bym to tak robił

Mila: Dobranoc Panowie

ZKS: Dobranoc i Pani.

Metis: Trochę się pogubiłem

	1
Czyli nie ma sensu w nierównościach zamieniać postaci: cos3x≤−		do postaci:
	2

	π
cos3x≤cos(		+π) ?
	3

ZKS: Dobra też zaraz lecę się wykąpać i do łóżka, bo jutro muszę sprezentować prezentację.

ZKS: Spójrz Mila napisała to samo.

Metis:

	1
Trochę nie rozumiem po co Nam cosu=
	2

Metis: Już rozumiem

Metis: Do wyznaczenia rozwiązań cosu=−1/2

mat: Czy moja odpowiedź jest w końcu dobra to co napisałem czy też robię jakiś błąd

Metis: Trzymaj się ZKS Dobranoc Milu

Metis: mat trzeba pomnożyć *3.

ZKS: Podzielić. Też się trzymaj Metis.

mat: co ? jak pomnożyć jaka tu powinna byc odpowiedź w końcu ?

mat: już to przecież wcześniej podziliłem

Evelek:

	1
cos3x ≤ −
	2

Ja bym podstawil zmienną t = 3x

	1
Mamy cos t ≤ −
	2

Odczytujemy zbiór rozwiązań a potem wracamy do naszej zmiennej: 3x ≤ nasze rozwiązanie Dzielimy na trzy i mamy to samo.

Metis: A racja sory , podzielić

Mila:

	2π		2πk		4π		2πk
x∊<		+		,		+		>
	9		3		9		3