wartość bezwzględna, równania Mariusz: Równanie |m−x|+|x−5| = 9 ma nieskończenie wiele rozwiązań dla: jest to zadanie zamknięte z odpowiedziami m=−14, m=4, m=5, m=14, odpowiedź to 14 doszedłem do tego podstawiając podane liczby do równanie ale jak to mądrze zapisać jeżeli trafi mi się to w zadaniu otwartym?

Evelek: Czy 14 to na pewno prawidlowa odpowiedz? Podstawmy x = 0. Otrzymamy 14 + 5 = 19, a nie 9.

yht: "nieskończenie wiele rozwiązań" nie oznacza że musi być x∊R, dla m=14 rozwiązaniem będzie x∊<5,14> a w takim przedziale jest nieskończenie wiele liczb więc poprawna odp to m=14 w zadaniu otwartym możesz np. rozwiązać graficznie : |m−x|+|x−5| = 9 |x−m| = 9 − |x−5| |x−m| = − |x−5| + 9 f(x) = g(x) rysujesz g(x) − zaczynasz od |x|, potem symetria S_OX, na koniec translacja o wektor [5,9] zaś f(x) − przesuwasz |x| o (m) w prawo, odczytujesz takie (m) żeby f(x) częściowo "nałożyło się" na g(x) − piszesz "dla m=... wykresy funkcji się pokrywają w nieskończenie wielu punktach, stąd równanie f(x)=g(x) ma dla m=... nieskończenie wiele rozwiązań"

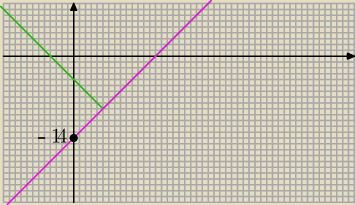
Jerzy: Tutaj masz interpretację graficzną.... prosta y = x − 14 począwszy od pewnego x. pokrywa sie z wykresem: y = Ix−5I − 9