ekstrema Paweł: Dobry wieczór , mógły ktoś podrzucić z jakieś dwa zadania na ekstrema? Maksymalna minimalna objętość stożka itp? Poziom matura rozszerzona.

5-latek : W dany stożek wpisac walec o najwiekszsej powierzchni bocznej Rysunek wykonać samemu

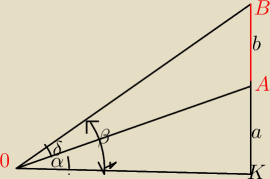
5-latek : Zadanie nr 2 na pionowej scianie powyżej poziomu oczu obserwatora wisi plakat AB W jakiej odleglosci od sciany powinien stać obserwator aby kat δ pod którym widzi on plakat był największy . Tyle starczy

5-latek : Rysunek do zadania oczywiście samemu zrobić

Metis: 5−latku może dajmy Pawłowi trochę bardziej maturalne?

5-latek : Metis To sa zadania maturalne . Nie ma potrzeby stosować w nich rachunku różniczkowego

Paweł: 5−latku mógłbyś podać odpowiedzi do tych zadań? Jakbym miał problemy albo błędne wyniki to się do Was złosze

Paweł: Chociaż z typem zadania maturalnego jak zadanie 2 spotykam sie pierszy raz, a troche tych arkuszy już przerobiłem

5-latek : DO 1 zadania R−promien stożka H wysokość stożka r i h to promien i wysokość szukanego walca

	H
Wysokosc szukanego walca h0=		(R−r0)= 0,5H
	R

DO drugiego (masz rysunek x−odleglosc to x_max=√ab

Paweł: Dzięki !