Matematyka liceum misio: W trójkąt równoboczny wpisano dwa okręgi styczne zewnętrznie do siebie, każdy o promieniu 2 cm. Oblicz długość boku tego trójkąta.

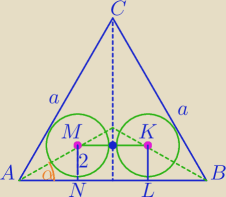
Mila: α=30^o W ΔANM:

	2
tg(30o)=
	|AN|

√3		2
	=
3		|AN|

Mila: cd. √3*|AN|=6 /*√3 3|AN|=6√3 |AN|=2√3 2*2√3+4=a a=4*(√3+1) ========

Jack: Miluskad wiemy ze α=30?

misio: Chodzi o rozwiązanie bez użycia tangesa

misio: ?

Mila: 1) Środek okręgu wpisanego w Δ leży na przecięciu dwusiecznych kątów . AM^→jest dwusieczną kąta A, |∡A|=60^o 2) Bez tangensa?: ΔANM to trójkąt o kątach 30,60, 90. ∡M=60^o⇔|AM|=4 4²=2²+|AN|² |AN|=√12=2√3 ==================

Mila: Misio zadaje pytania i nie czyta?

Jack: wszystko jasne ; D