Matura Cleo: Jakie wzorów nie ma w karcie wzorów maturalnych ,a są pomocne na maturze ?

Red: Z pewnością na współczynnik kierunkowy a: Y₁ − Y₂ a= ___________ X₁ − X₂

Eta: 1/ Ilość przekątnych w wielokącie wypukłym o n −− bokach

	n(n−3)
d=
	2

2/ suma kątów wewnętrznych wielokąta wypukłego o n bokach s=(n−2)*180^o 3/ ciągi : wzór ogólny ciągu o danej sumie S_n a_n= S_n−S_n−1 4/ wzory na błąd względny i błąd bezwzględny B_b= |wartość rzeczywista − wartość przybliżona|

	Bb
Bw=
	wartość rzeczywista

B_w % = B_w*100%

Metis: Na forum "gdzieś" jest obszerny post, w którym kiedyś zbieraliście takie przydatne "fajne" wzory i twierdzenia, których albo w podstawie nie ma, albo nie ma w kartach Tylko gdzie?

Metis: Jeśli mamy A(x₁, y₁) i B(x₂, y₂) należące do danej prostej, to współczynnik kierunkowy tej prostej:

	y2−y1
a=
	x2−x1

Eta: Koniecznie przy założeniu ,że x₂≠x₁

Metis: Dokładnie

Evelek: Dorzucę od siebie: Pole równoległoboku to takze 1/2 * d₁ * d₂ * sinα, gdzie α to kąt przecięcia sie przekątnych d₁ i d₂. Rano dopisze więcej bo mam wypisane.

Metis: Pole trójkąta metoda wyznaczników jeszcze

Dk.: wzór Herona + 1000 jeszcze innych ale nie martw się masz duże szanse żeby i bez nich zdać ok. 75 %

Evelek: Pole czworokąta: 1/2 * r * (a+b+c+d) gdzie r to promień koła wpisanego.

	360
Pole dowolnego n−kąta foremnego: 1/2 * n * sin		, gdzie n to ilość ścian czyli np.
	n

szesciokat ma 6 sześć ścian.

mock: a jakies typowo na rozszerzenie przydatne, (oprocz vietta 3.st)?

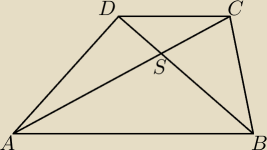
yht: P_ΔASD = P_BSC gdzie ABCD, dowolny trapez, a S punkt przecięcia przekątnych AC i BD tego trapezu a^log_bc = c^log_ba dla a,b,c>0 oraz b≠1

yht: P_ΔASD = P_ΔBSC

Evelek: Gdy mamy trapez równoramienny ABCD i potrzebujemy wyznaczyć długość odcinka łączącego oba ramiona który przedzieli ten trapez na dwa trapezy o tych samych polach stosujemy wzór:

	a2 + b2
x = √
	2

Pierwiastek ten dotyczy całego równania po prawej stronie. a, b − podstawy trapezu x − odcinek łączący ramiona rownolegly do podstaw trapezu Jesli zaś chcemy wyznaczyć długość odcinka laczacego srodki obu ramion trapezu rownoramiennego to stosujemy wzór:

	a + b
x =
	2

Pierwszy wzór to tak zwana srednia geometryczna. Drugi wzór to srednia arytmetyczna.

5-latek :

	tgα
sinα=
	√1+tg2α

	1
cosα=		jeśli masz dany tgα
	√1+tg2α

tgα*ctgα=1

	1
1+tg2α=
	cos2α

	1
1+ctg2α=
	sin2α

qulka: pomijając to że matury są pisane pod tablice więc na sam egzamin są potrzebne tylko wzory z tablic

mock: ale czasami niektóre wzory, ktorych nie ma w tablicach potrafią zaoszczedzić mnóstwo czasu a może i punktów, bo eliminują sporo dodatkowych obliczeń, przy których można by coś walnąć rachunkowo np. wzory vietta 3st.

mock: viete'a*

qulka: i były w jakimś zestawie maturalnym bo nie przypominam sobie żebym widziała takie zadanie

mock: m.in miałem ostatnio w probnej maturze z pazdro a jesli uwzglednic matury majowe, to tak sie sklada, ze w zeszlorocznej maturze okazały się przydatne

Benny: Jakoś nie przypominam sobie abym ich używał.

qulka: pazdro to nie CKE

mock: dlatego też napisałem, że "czasami niektóre wzory, ktorych nie ma w tablicach potrafią zaoszczedzic" i faktycznie mozna bylo sie obejsc bez tych wzorow, ale to nie znaczy, ze nie mozna bylo sobie troche oszczedzic rachunkow dlatego, tez nie rozumiem twojego komentarza Benny, bo liczy sie kazdy poprawny sposob rozwiazania no chyba, ze twoje rozwiazanie jest jedynym poprawnym sposobem jaki istnieje

Benny: O które zadanie chodzi?

qulka: zwłaszcza że matury są pisane pod tablic i najprostsze sposoby na te zadania to zastosować odpowiedni wzór z tablic ale owszem..taka powtórka wzorów zawsze się przyda jak chcemy studiować coś z matematyką w tle

yht: Benny, chodzi o zadanie 15 z matury rozsz. maj 2015