Mila:
| | −x3+3x2+4x−12 | |
f(x)= |
| |
| | x3−7x−6 | |
D:
x
3−7x−6≠0
W(x)=x
3−7x−6 szukamy pierwiastka wśród liczb: {±1,±2,±3,±6}
W(1)=1−7−6≠0
W(−1)=−1+7−6=0
x=−1 jest pierwiastkiem W(x)
Schemat Hornera x=−1
1 0 −7 −6
1 −1 −6 0
x
3−7x−6=(x+1)*(x
2−x−6)
Δ=25
| | 1−5 | | 1+5 | |
x= |
| =−2 lub x= |
| =3 |
| | 2 | | 2 | |
x
3−7x−6=(x+1)*(x+2)*(x−3)
D=R\{−2,−1,3}
Licznik:
P(x)=−x
3+3x
2+4x−12
P(−1)=1+3−4−12≠0
P(−2)=8+12−8−12=0
x=−2 jest pierwiastkiem P(x)
−1 3 4 −12
−1 5 −6 0
P(x)=(x+2)*(−x
2+5x−6)
Δ=1
x=2 lub x=3
P(x)=(x+2)*(−1)*(x−2)*(x−3)
| | (x+2)*(−1)*(x−2)*(x−3) | |
f(x)= |
| |
| | (x+1)*(x+2)*(x−3) | |
Eta:
Inny sposób
Mianownik :
x
3−x−6x−6 = x(x
2−1) −6(x+1)= x(x+1)(x−1)−6(x+1) =(x+1)(x
2−x−6)= (x+1)(x−3)(x+2)
D= R\{−1,3,−2}
Licznik:
−x
2(x−3) +4(x−3) = (x−3)(4−x
2)= (x−3)(2−x)(2+x)
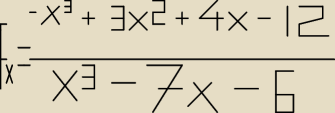 Zapisz wzór funkcji w najprostszej postaci.
Zapisz wzór funkcji w najprostszej postaci.

