Twierdzienie sinusów typ: Wyprowadź twierdzenie sinusów, wiedząc, że suma niewspółiniowych wektorów a, b, c tworzących trójkąt wynosi zero.

typ: Pomoże ktoś?

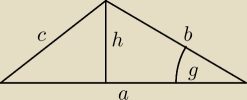
g: A może inaczej. Pole trójkąta to połowa iloczynu długości dwóch boków i sinusa kąta między nimi. (rysunek: h = b*sinγ; P = 1/2 a*h = 1/2 a*b*sinγ) P = 1/2 a*b*sinγ = 1/2 b*c*sinα = 1/2 c*a*sinβ Dzielimy te równania przez 1/2 a*b*c i dostajemy:

sinγ		sinα		sinβ
	=		=
c		a		b

typ: Niestety nie, to zadanie muszę rozwiązać wykorzystując wektory oraz iloczyn wektorowy tak, jak podałem w zadaniu. Wciąż nie wiem, jak to zrobić, dlatego proszę o pomoc.