#workout PrzyszlyMakler: W prostokącie ABCD punkt P jest środkiem boku BC, a punkt R jest środkiem boku CD. Wykaż, że pole trójkąta APR jest równie sumie pól trójkątów ADR oraz PCR. Spróbuje ktoś? I rady na rozwiązywanie dowodów geometrycznych mile widziane!

Eta: Żartujesz? ( to poziom gimnazjum

Jack: hehe, przejmuje?

Jack:

	1
PΔADR =		* 2x * y = xy
	2

	1
PΔPCR =		xy
	2

	1
PΔABP =		* 2y * x = xy
	2

P_ΔAPR = P_prostokata − P_{tych 3 trojkatow}

	1
PΔAPR = 2x * 2y − (xy +		xy + xy)
	2

	5		3
PΔAPR = 4xy −		xy =		xy
	2		2

	3
PΔADR + PΔPCR =		xy
	2

zatem

	3
P{ΔAPR = PΔADR + PΔPCR =		xy
	2

Jack: to naprawde jest gimnazjum ^^

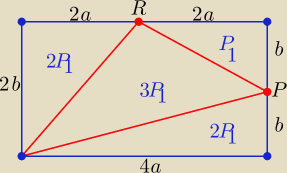
Eta: P= 8ab= 8P₁

Jack: tak tak ; D

PrzyszlyMakler: Racja, ale z zasady nie wiem co robić przy dowodoach geometrycznych. Sa straszne.

PrzyszlyMakler: Dziękuję.