Pytanie do maturzystow Janko: z jakimi działami macie największe problemy?

tamka: Żadnych problemów ( bo matura już za 11 dni

regena97: Rachunek prawdopodobieństwa..

ICSP: Probabilistyka. Kompletnie mi ten dział nie wchodzi do głowy

Janko: Mam fajne zadanko. Dany jest trójkąt ABC, w którym bok BC jest dwa razy dłuższy od boku AB, a kat ABC jest dwa razy większy od kąta BAC. Pokaż, że |AC|² = 6 |AB|²

Janko: Ktoś coś?

mat 4: Sprawdź dokładnie treść zadania !

Janko: Dokładnie taka, zadanie za 7 pkt

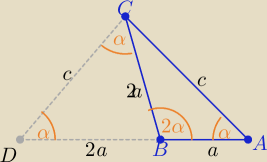
Eta: |AC|=c , |AB|=a Po odłożeniu odcinka |BC|=2a trójkąt BDC jest równoramienny o kątach α,α oraz równoramienny jest trójkąt DAC o kątach α, α zatem z podobieństwa tych trójkątów z cechy (kkk)

c		2a
	=		⇒ c2=|AC|2= 6a2 =6|AB|2
a+2a		c

c.n.w

Lech Roch: A dalo sie skorzystac w jakis sposob z twierdzenia cosinusow w tym wypadku?

Eta: Ja "chodzę" zwykle najkrótszą drogą A Ty jak chcesz ?................ to jedź z Gdańska do Sopotu przez Rzym

Lech Roch: Bylbym wdzieczny jakbys rozpisala z twierdzenia cos bo na dorysowanie drugiego trojkata niestety nie wpadlbym a I jeszcze pytanko skad wiesz ze kat przy wierzcholku d jest taki sam jak przy a?

yht: dało się, z kombinacji tw. sinusów i cosinusów

	AC		BC
najpierw z tw. sinusów		=		z tego dostajesz AC = 4a*cosα
	sin2α		sinα

i później z cosinusów BC² = AB²+AC² − 2*AB*AC*cosα wyjdzie 4a² = a² + 16a²*cos²α−8a²*cosα dzieląc stronami przez a² otrzymamy 4 = 1+16cos²α−8cos²α

	√3		√3
z tego wyjdzie że cosα=		bądź cosα=−		z czego ujemny cosinus nie może
	√8		√8

być bo wtedy bok AC wyjdzie na minusie

	√3		√3
zatem cosα=		, czyli AC = 4a*
	√8		√8

	3
AC2 = 16a2*		= 6a2
	8

6AB² = 6 a² zatem AC² = 6AB²

Lech Roch: <3