Trudne zadanie optymalizacyjne harry: Rozważmy zbiór ostrosłupów prawidłowych czworokątnych o krawędzi bocznej długości 6. Wyznacz długość krawędzi podstawy tego ostrosłupa, którego pole przekroju płaszczyzną wyznaczoną przez środki dwóch sąsiednich krawędzi podstawy i wierzchołek ostrosłupa jest największe. Oblicz największe pole przekroju. 3 razy próbowałem to zrobić, nie wychodzi odp.x=4√3 P(4√3)=6√3

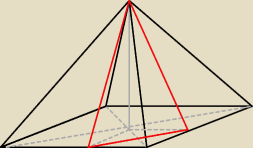
yht: dł. krawędzi podstawy = a przekrój − czerwony trójkąt równoramienny podstawę b czerwonego przekroju liczę z pitagorasa: (a/2)² + (a/2)² = b²

	a*√2
z tego mam b =
	2

ramię c czerwonego przekroju liczę z pitagorasa: c² + (a/2)² = 6² c = √36−a²/4 wysokość h przekroju liczę z pitagorasa: h² + (b/2)² = c²

	a*√2		a2
h2 + (		)2 = 36−
	4		4

	a2		a2
h2 +		= 36 −
	8		4

h = √36−3a²/8 Pole przekroju:

	1		1		a*√2
P =		b*h =		*		* √36−3a2/8
	2		2		2

	a*√2
P =		*√36−3a2/8
	4

P = √(a*√2/4)² * √36−3a²/8 P = √a²/8 * (36−3a²/8) obliczam pochodną funkcji podpierwiastkowej

	a		3a2		a2		−3a
g'(a) =		*(36−		) +		*(		)
	4		8		8		4

	3a3		3a3
g'(a) = 9a −		−
	32		32

	3a3
g'(a) = 9a −
	16

	3a3
g'(a) = 0 → 9a−		=0 |*16
	16

144a−3a³=0 |:3a 48−a² = 0 a² = 48 a = √48 = 4√3 P = √a²/8 * (36−3a²/8) P = √48/8 * (36−3*48/8) = √6*(36−18) = √6*18 = √108 = 6√3

maturzysta: Też sobie przepiszę i popatrzę jak to zrobiłeś bo podobne są na maturze.

harry: Dzięki wielkie Te zadania są na maturze za 7 punktów więc mam nadzieję, że uda mi się zrobić.