Trójkąty
Pati18773: Oblicz promień okręgu wpisanego w trójkąt prostokątny wiedząc że środkowa poprowadzona z
wierzchołka kąta prostego ma długość 5 cm a stosunek długości przyprostokątnych trójkąta
wynosi 1:2.
Nie wiem jak wykorzystac ta środkowa. Próbowałam robić ale wyszło mi rownanie z dwiema
niewiadomymi

Ktoś wytłumaczy ? Proszę

24 kwi 16:57
Pati18773: Ktoś da radę jak zrobić ?
24 kwi 17:11
yht:
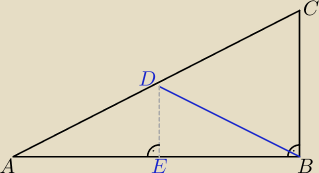
z treści zadania:
|AB| = 2x, |BC| = x
|BD| = 5
|AD| = |CD|
jeśli dorysujesz sobie odcinek DE równoległy do BC, to okaże się że trójkąty ADE i ABC są
| | |AD| | | 1 | |
podobne, oraz |
| = |
| |
| | |AC| | | 2 | |
| | |DE| | | 1 | | |AE| | |
zatem (ze względu na podobieństwo) musi być |
| = |
| oraz |
| = |
| | |BC| | | 2 | | |AB| | |
| | 1 | | x | |
|
| czyli |DE| = |
| oraz |AE|=x, |EB|=x |
| | 2 | | 2 | |
Odc. DE jest wysokością trójkąta ABD.
Ponieważ E jest środkiem odcinka, zaś wysokość DE spada na środek podstawy AB, to trójkąt ABD
musi być równoramienny, zatem musi być |AD|=|BD|
czyli |AD|=5, |CD|=5, |AC|=10
Pitagoras w trójkącie ABC (z jedną niewiadomą) załatwia całe zadanie
24 kwi 17:14
Pati18773: Dziękuję bardzo już wszystko jasne !

24 kwi 17:17
E:
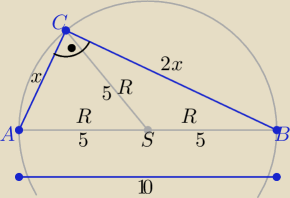
R =|CS| −−−− długość okręgu opisanego na trójkącie prostokątnym
| | 1 | |
|AB|=c=2R= 10 , ( masz w tablicach wzór R= |
| c |
| | 2 | |
b=|AC|=x, a= |BC|=2x , x>0
z tw. Pitagorasa : x
2+4x
2=10
2 ⇒ x
2=20 ⇒ x= 2
√5
| | a+b−c | |
r −−− długość promienia okręgu wpisanego r= |
| ( wzór z tablic |
| | 2 | |
24 kwi 17:51
 Ktoś wytłumaczy ? Proszę
Ktoś wytłumaczy ? Proszę 
 z treści zadania:
|AB| = 2x, |BC| = x
|BD| = 5
|AD| = |CD|
jeśli dorysujesz sobie odcinek DE równoległy do BC, to okaże się że trójkąty ADE i ABC są
z treści zadania:
|AB| = 2x, |BC| = x
|BD| = 5
|AD| = |CD|
jeśli dorysujesz sobie odcinek DE równoległy do BC, to okaże się że trójkąty ADE i ABC są

 R =|CS| −−−− długość okręgu opisanego na trójkącie prostokątnym
R =|CS| −−−− długość okręgu opisanego na trójkącie prostokątnym