Kwadratowa Oliwia: Ostatnie zadanie na dzisiaj bo juz mam dość Wyznacz możliwie najszerszy przedzial do którego należy liczba p i możliwe najszserszy przedzial do którego należy liczba q jeśli pierwiastki trójmianu y=x²+px+q spelniaja nierownosci −5<x₁<−4 2<x₂<3 Tutaj nie wiem jak podejść do tego zadania

Jerzy: Musi być: f(−5) > 0 i f( −4) < 0 i f(2) < 0 i f(3) > 0

Oliwia: A cos więcej aby zrozumieć Dlaczego tak ?

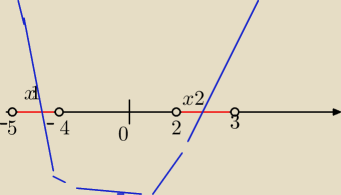
Oliwia: Narysowalam sobie na osi liczbowej taki szkic

Jerzy: I teraz widać, skąd te warunki oczywiście Δ > 0

Oliwia: dziekuje czyli x₁ i x₂ nie musze wyznaczać ?

Jerzy: Nie

Oliwia: wyszlo mi tak 25−5p+q>0 16−4p+q<0 4+2p+q<0 3+3p+q>0 Nie umiem za bardzo sobie z ty poradzić na chwile obecna

Oliwia: Ostatnia nierownosc 9+3p+q>0

Oliwia: Odpowiedz do zadania jest taka 1<p<3 −15<q<−8

yht: zrób (nietypowy) układ współrzędnych − nie taki x,y tylko p,q narysuj w nim funkcje liniowe q=5p−25, q=4p−16 itd. potem zakreskuj obszary (jeśli w nierówności będzie > to obszar nad prostą, jeśli < to pod prostą) i na koniec zobacz jaka będzie część wspólna wszystkich 4 nierówności

Oliwia: Pomozesz Jerzy dokonczyc to zadanie ? Bardzo prosze

Oliwia: Dzieki yht Tak zrobie jak piszesz ale musze jednak wypocząć. To chyba z tego względu to zadanie było oznaczone jako trudne

yht: możesz to zadanie zrobić też korzystając z wzorów Vieta −p = x₁+x₂ q = x₁*x₂ ze względu na warunki patrzysz jaka może być najmniejsza i największa suma x₁+x₂ najmniejsza: musi być x₁=−5, x₂=2, wtedy x₁+x₂=−3 największa: x₁=−4, x₂=3, x₁+x₂=−1 czyli −p∊(−3,−1) stąd p∊(1,3) to samo z iloczynem, najmniejszy i największy, potem q∊ ...

Oliwia: najmniejszy lioczyn będzie dla x₁=−5 x₂=3 będzie wtedy −15 Naj większy iloczyn będzie dla x₁=−4 x₂=2 będzie wtedy −8 wtedy q należy (−15,−8) dziekuje CI za pomoc