Kwadratowa Oliwia: Dla jakiej wartości parametru m dziedzina funkcji f(x)=√m²+1+mx−x² zawiera przedzial domknięty <0,4> −x²+mx+m²+1≥0 Δ=b²−4ac Δ=m²−4*(−1)*(m²+1) Δ= m²+4m²+4 =5m²+4 Wyznaczam m₁ i m₂

	−b−√Δ
m1=
	2a

	−m−√5m2+4		1		1		1
m1=		=		m+		√5m2+4=		(m+√5m2+4)
	−2		2		2		2

	−b+√Δ
m2=
	2a

	−m+√5m2+4		1		1		1
m2=		=		m−		√5m2+4=		(m−p{5m2+4)
	−2		2		2		2

	1		1
m należy <		(m−√5m2+4) ,		(m+p{5m2+4)
	2		2

Dziedzine wyznaczyłam ale nie wiem jak z tym warunkiem dalej

Oliwia: Ktos podpowie w tym zadaniu ?

ICSP: Wystarczy aby g(0) ≥ 0 i g(4) ≥ 0 gdzie g(x) = −x² + mx + m² + 1

Oliwia: Dziekuje Tobie czyli mam rozwiazac te dwie nierownosci i wyznaczyć czesc wspolna rozwiazan Czyli w sumie niepotrzebnie wyznaczałam dziedzine te funkcji ? g(0)≥0 0²+m*0+m²+1≥0 m²+1≥0 ale to jest zawszse >0 czyli mam zapisac ze m należy do R ? g(4)≥0 −(4)²+m*4+m²+1≥0 −16+4m+m²+1≥0 m²+4m−15≥0 Δ=b²−4ac Δ=16+60=76

	−4−√76		1
m1=		=−2−		√76 <0
	2		2

	−4+√76		1
m2=		= −2+		√76>0
	2		2

m należy (−∞ ,−2−0,5√76>U<−2+0,5√76,∞) Rozwiazaniem jest ten ostatni przedzial Jeśli możesz to napisz dlaczego dales takie warunki ?

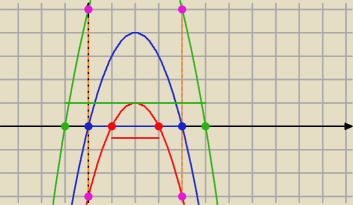
ICSP: Przestudiuj rysunek i zastanów się które parabole są dobre a które nie. Poziome kreski to przedział dziedziny.

Oliwia: Niebieska i zielona parabola jest dobra czerwona natomiast nie

ICSP: i spójrz na wartości w punktach f(0) i f(4).

prosta: popatrzcie też na wierzchołek

ICSP: prosta co ma tutaj wierzchołek do rzeczy ?

Oliwia: Już widze . One sa ≥0 dzięki za wyjaśnienie

prosta: najwyraźniej wierzchołek w tym wypadku nie jest istotny