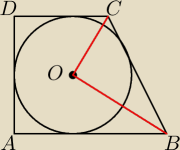
Planimetia DSAA: Jak udowodnic ze kat COB jest katem prostym?

W: Półproste BO oraz CO to dwusieczne kątów, to wynika z tego, że O to środek okręgu wpisanego w trapez.

	π		π
Teraz |∠CBO| + |∠BCO| = 0.5 (|∠CBA| + |∠BCD|) =		, czyli |∠BOC| =		, QED.
	2		2

jc: Może istnieje jakiś sprytny sposób, ale na pewno można liczyć kąty. kąt DCO = kąt OCB = 1/2 * kąt DCB kąt ABO = kąt OBC = 1/2 * kąt ABC dodajemy stronami kąt OCB + kąt OBC = 1/2 * 180^o = 90^o Dlatego kąt BCO = 180^o − kąt OCB − kąt OBC = 90^o To nie jest ładne rozwiązanie, ale jest.

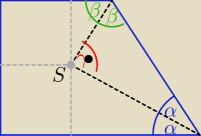
Eta: w każdym trapezie : 2α+2β=180^o ⇒ α+β=90^o to γ=90^o

DSAA: o takie coś mi Eta chodziło Dzięki wielkie!

jc: