trójkąt ostrokątny Justyś: Wykaż, że jeśli a,b,c są długościami boków trójkąta ostrokatnego takimi, że a<b<c oraz α,β,γ są miarami kątów tego trójkąta leżącymi odpowiednio na przeciwko boków a, b,c , to tgα<tgβ<tgγ.

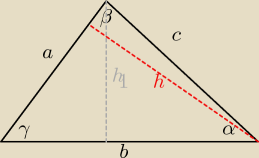
Godzio: a<b<c

	h*a		h1*b
P=		=		=
	2		2

ha=h₁b

	ah
h1=
	b

	h1		h1		a2h2		1
tgα =		=		=		*		=
	b−(a2−h12)		b−a2+h12)		b2		a2h2   b−a2 +   b2

U{

	h
tgβ=
	a−(b2−h2)

	h
tgγ=
	a−(c2−h2)

Godzio: czekaj niechcacy mi sie wyslalo jeszcze dokanczam

Godzio: poddaje sie kombinowałem ale jednak nic z tego ktoś inny napewno Ci pomorze tutaj i tak początek troche zawaliłem

Justyś: ale mimo wszytko dzieki za pomoc moze mi tez cos wyjdzie

Eta: Myślę,że najprościej tak w trojkącie na przeciw najdłuższego boku leży kąt , który ma najwiekszą miarę więc jeżeli a<b<c to: α<β<γ ponieważ trójkąt jest ostrokątny , to α,β,γ €(0,90^o) a funkcja tg −−− jest rosnąca to i tgα<tgβ<tgγ c.b.d.o