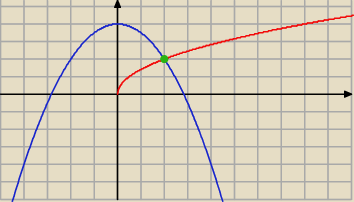
Punkty przeciecia Laura: Witam. Wie ktoś może jak obliczyć punkt wspólny dla dwóch funkcji? Wiem, że, na wykresie widać, że to 2,2, ale jak to obliczyć ? f (x)= −1/2x² +4 g (x)= √2x Må ktoś jakiś pomysł?

maturzysta: f(x) = g(x) działaj.

Laura: To ✌ ja wiem tylko nie wiem jak z tego pierwiastka z 2x coś mądrego wywnioskować? BTW takim sposobem nie da się nic obliczyć. Zresztą spróbuj sam

5-latek : −0,5x²+4=√2x dla x≥0 Obie strony do potęgi drugiej (−0,5x²+4)²=2x dalej Ty

maturzysta: Rozwiązałem, wszystko się zgadza.

Laura: A ja nie wiem jak to rozwiązać 0,25 x⁴−4x²+16−2x=0

ICSP: Podziel przez (x−2) a potem zastosuj wzory Cardano.

maturzysta: Stronami pomnożyć przez 4. Otrzymujemy x⁴ − 16x² − 8x + 64 = 0 Równość ta jest równa dla x = 2. Duży ten wyraz wolny tylko...może ktoś ma jakiś szybki sposób na ogarnięcie czegoś takiego...

5-latek :

1
	x4−4x2+16−2x=0 (mnoze przez 4 obie strony równania
4

x⁴−16x²−8x+64 =0 Może i można tu grupować (ja nie wiem jak Wobec tego licze W(1)≠0 w(2)=0 (x⁴−16x²−8x+64):(x−2)= x³+2x²−12x−32 x³+2x²−12x−32 =0 Na poziomie liceum (bo do niego chodzisz ) nie mamy pierwiastkow całkowitych Wobec tego mamy tylko x=2 Podstawiam x=2 do np. wzoru funkcji g(x) g(x)= √2*x= √2*2= 2 Mam punkt przciecia P=(2,2)

Jurek: Czy g(x) = √2 x czy g(x) = √2x ?

Jerzy: g(x) = √2x to funkcja liniowa

Jurek: Pytałem Laurę, bo może w treści zadania jest własnie funkcja g(x) = √2 x

ICSP: Bez różnicy. x = 2 jes jedynym rozwiazaniem równania : −0,5x²+4=√2x

Jurek: Jest różnica w sposobie wyznaczenia współrzędnych wspólnego punktu wykresów. W przypadku g(x) = √2 x mamy równanie kwadratowe, a nie równanie 4 stopnia.

Laura: √2x Jerzy, Oba pod pierwiastkiem

Laura: najsmieszniejsze, ze to zadanie za 5%

5-latek : Przeciez to zadanie jest latwe Należy umiec rozwiazywc takie równania wielomianowe Jak nie grupowanie to twierdzenie o pierwiastkach ch całkowitych lub wymiernych Przepraszam ale jak chcesz studiować nawet w Danii jeśli tego nie potrafisz ?

5-latek : Lauro A najsmieszniejszse jest to ze jak widzisz my już w przedszkolu takie równania rozwiązujemy

Laura: Nie da sie pogrupowac, zeby mialo sens i dawalo jakies sensowne informacje. A z ta metoda prob i bledow tez mi sie nie widzi... Rownie dobrze, mozna bylo to zauwazyc na wykresie. Tam jest wyraznie napisane OBLICZ. Wiec ja sadze, ze musi byc jakas inna metoda niz proby i bledy

Laura: Mhm, tylko ja nie chce studiowac matematyki raczej. Tylko radiografie lub inzynierie oprogramowania

5-latek : To w takim razie muszse z przykroscia stweirdzic ze jeśli piszsesz metoda prob i bledow to nieznasz tw Bezout i Tw o wymiernych pierwiastkach równania . Jest mi z tego powodu przykro

Laura: W(1)≠0 w(2)=0 to jest metoda prob i bledow.

5-latek : Ja myslaem ze w Danii matematyka stoi na wysokim poziomie Nawet Janek 191 kazal mi czytac Twoje posty Ale widze ze jest jeszcze gorzej niż u nas . Z takimi wiadomościami (nie krytykuje Ciebie tutaj ) ale u nas po 1 polroczu −jeśli nie sa prywatne wypadasz . Nie wiem jak tam jest ale jeśli inzynieria oprogamowania to tym bardziej matematyka . Po prostu . Nie wiem co mam sadzic o tym . Może już nie będę pisal ?

Laura: hmmm. Ja chodzilam do technikum w Polsce i nic takiego nie mialam, zadnych twierdzen, ani niczego. Nie wiem jak bylo za komuny bo troche mlodsza jestem, ale widocznie sie bardzo pogorszylo. A mature zdawalam w Polsce w 2013 roku. A w ogole o co Ci chodzi? Nie wiem, czy mi czegos zazdroscisz czy cos skoro wytykasz mi niewiedze? Ja zaczelam sie uczyc tutaj matematyki od stycznia. A, ze mam braki to wiem, nie mowie, ze tak nie jest. W Danii jest duzo wyzszy poziom niz w Polsce i dlatego min. pisze na forum, zeby zrozumiec, nauczyc sie i zaliczyc wszystko Nie wiem skad w Tobie taka antypatia wobec mnie... Mam nadzieje, ze masz po prostu zly dzien i jutro juz bedziesz mily

Laura: A i na inzynierii oprogramowania (informatyka) nie ma juz praktycznie zadnej matematyki poza poziomem szkoly podstawowej (moj narzeczony skonczyl ten sam kierunek i teraz pracuje po nim), wiec nie mam sie co martwic. Na radiografii tym bardziej.

5-latek : To w takim razie powodzenia A na zdrowie