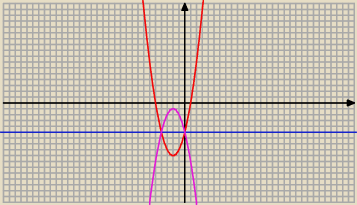
symetria funkcji kwadratowej maturzysta: Mamy funkcje kwadratową: y = x² + 4x − 5 Mam zrobić symetrię względem prostej y = −5. Mój pomysł jest taki: Znajduje wierzchołki tej paraboli, w tym wypadku będzie to W(p,q) = (−2 , −9). Rysuje sobie schematyczny wykresik, interesują mnie tu tylko wierzchołek i prosta y = −5. Znajduje odległość między q (−9) oraz prostą y = −5. Wynosi ona 4. Czyli symetria tej paraboli będzie, gdy wierzchołek będzie w punkcie W(p,q) (−2 , −1). Wstawiam ten wierzchołek do postaci kanonicznej funkcji kwadratowej i otrzymuje y = (x + 2)² − 1, czyli y = x² + 4x + 3. Skoro to ma być symetria względem y = −5 czyli względem osi X,to jeszcze zmieniam współczynnik przy a, otrzymuje −x² + 4x + 3. I tu moje pytanie, w odpowiedziach mam: y = −x² − 4x − 5. Czego tu jeszcze nie rozumiem?

Janek191: y = x² + 4 x − 5

	−4
p =		= − 2
	2

q = f(−2) = 4 − 8 − 5 = − 9 W = ( − 2, − 9) S = ( − 2, − 5) jest środkiem odcinka W W' W ' = ( −2, y) więc

− 9 + y
	= − 5 ⇒ − 9 + y = − 10 ⇒ y = − 1
2

więc W' = ( − 2, − 1) y = a*( x + 2)² − 1 A = ( 0, − 5) − 5 = a*( 0 + 2)² − 1 = 4 a − 1 ⇒ 4a = − 4 a = − 1 Odp. y = − ( x + 2)² − 1 ================== lub y = − x² − 4 x − 5 =============

maturzysta: Kurczę...czyli identyko jak moje tylko ja tego punktu nie podstawiłem tylko od razu przyjąłem współczynnik a jako −1. Tego minusa jednego zabrakło przed nawiasem w kanonicznej i wszystko się zgadza... Dziękuję Janku.