trójkaty
Metis: Jak najszybciej policzyć pole Δ znając jego niewymierne długości boków?
22 kwi 21:17
*.*: Może wzorem Herona? Zależy jakie są liczby.
22 kwi 21:20
Metis: Niewymierne długości boków. Heron odpada.
22 kwi 21:21
*.*: a możesz podać te długości?
22 kwi 21:28
bezendu:
Jak chcesz naprawdę szybko to proszę trzymaj algorytm
function Heron(aA,aB,aC: double):string;
var
p,w: double;
begin
result:='Nie można zbudować trójkąta';
if((aA+aB>aC)and(aB+aC>aA)and(aC+aA>aB))then
begin
p:=(aA+aB+aC)/2;
w:=sqrt(p*(p−aA)*(p−aB)*(p−aC));
str(w:0:3,result);
end;
end;
22 kwi 21:29
g: Policzyć można wzorem Herona. Tobie chodzi prawdopodobnie o uproszczenie wyrażenia.
22 kwi 21:30
Mila:
Napisz zadanie, wszystko zależy, jakie to dane .
Można obliczyc sinus kąta między bokami.
22 kwi 21:34
Mariusz:
Sinus kąta między bokami .. tak ale najpierw trzeba by skorzystać z tw cosinusów
a później jedynki trygonometrycznej aby dostać sinusa . Heron wydaje się najszybszy
22 kwi 22:06
Metis: bezendu jaki to jezyk
Python? czy C# ?
22 kwi 22:07
bezendu:
Delphi
22 kwi 22:09
Metis: Milu treść jest taka:
Oblicz pole Δ o bokach:
2√7, 4√2, 2√15
22 kwi 22:09
maturzysta: A gdyby do kwadratu te boki podnieść w równaniu na pole, cos by dalo?
22 kwi 22:12
jc: A może to trójkąt prostokątny? A wtedy ...
22 kwi 22:15
Jack: bo jest prostokatny xD
22 kwi 22:34
Metis: No wiem, można sprawdzić
Ale chodziło mi po prostu jak mając niewymierne boki obliczyć to pole
22 kwi 22:35
Saizou :
tw. cosinusów, a potem jedynka i wzór z sinusem na pole
(nie zawsze rachunki będą łatwe)
22 kwi 22:39
Mila:
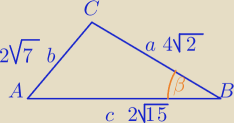
1) sprawdzić czy nie jest to Δ prostokątny− nie jest.
2) rysunek pomocniczy
2√7, 4√2, 2√15
a=4
√2
b=2
√7
c=2
√15
b
2=a
2+c
2−2a*c*cosβ
4*7=16*2+4*15−2*4
√2*2
√15*cosβ
potem sin β z jedynki tryg.
Przelicz jeszcze raz.
22 kwi 22:39
Metis: Dziękuję
Milu 
22 kwi 22:40
Eta:
Oblicz pole trójkąta o bokach długości :
√5 ,
√13 ,
√26
22 kwi 22:47
jc: Teraz ja nie rozumiem
(2
√7)
2 + (4
√2)
2 = (2
√15)
2
| | 1 | |
Pole = |
| * 2√7 * 4√2 = 4 √14 |
| | 2 | |
22 kwi 22:53
maturzysta: A mój sposób aby we wzorze P = √p(p−a)(p−b)(p−c) po wymnożeniu tego co pod pierwiastkiem,
podnieść do kwadratu aby pozbyć sie pierwiastka, a potem drugi raz do kwadratu aby pozbyć się
kolejnego pierwiastka, jest poprawny?
22 kwi 22:54
maturzysta: jc twoj sposób obliczenia to dokladnie polowa pola policzonego przez Mila.
22 kwi 22:56
jc: Eta
To trójąkąt wyznaczony przez wektory (5,1) i (3,2), a więc o polu (5*2−3*1)/2 = 7/2.
22 kwi 23:05
Mila:
Jc
No bo to jest trójkąt prostokątny, nie umiem tabliczki mnożenia i dodawania.
A
Metisek mnie nie sprawdził.
W każdym bądź razie, w przypadku, gdy nie jest prostokątny to można tak liczyć.
Wynik P taki sam jak u
JC.
22 kwi 23:14
Mila:
To znaczy zawsze można, ale w przypadku Δprostokątnego liczymy prościej, jak pokazano.
22 kwi 23:18
Eta:
Na poziomie 2 gimnazjum
P(ABCD)= 10 S= 10−(2,5+1+3) =
3,5
22 kwi 23:18
Metis: Milu przepraszam, ale zająłem się zadaniem od
zef
22 kwi 23:23
jc: Eta Toż właśnie to napisałem
Z punktu C wystają dwa wektory (5,1) i (3,2),
tyle, że nie umieściłem rysunku.
22 kwi 23:26
Marian : Aksjomat arkusz XI zadanie zamknięte?
22 kwi 23:27
maturzysta: Eta czy każdy trójkąt zarówno ostrokątny jak i rozwartokatny można wpisać w prostokąt i znaleźć
do niego odpowiednie długości boków aby się pierwiastki zgadzaly?
22 kwi 23:28
Metis: 
22 kwi 23:28
Metis: to do Mariana
22 kwi 23:28
Mila:
Metis, nic nie szkodzi, metoda może się przydać.
22 kwi 23:39
jc: maturzysta. Niby zawsze, ale jeśli chcesz mieć liczby całkowite, to nie.
7 nie jest sumą dwóch kwadratów liczb całkowitych.
22 kwi 23:44
Metis: Oczywiście, że się przyda
Dziękuje
23 kwi 00:06
Mila:
No to dobranoc
23 kwi 00:07
Metis: Dobranoc
Milu
23 kwi 00:11
Metis: Etuś i
jc Wam także Dziękuję
23 kwi 00:26