optymalizacja matematyka12: dłuższa podstawa trapezu równoramiennego ma długośc 4 cm, a jego obwód wynosi 10 cm. jaką długośc powinno mieć ramię tego trapezu, aby miał on największe pole. oblicz to pole

maturzysta: Juz ci wysyłam.

matematyka12: To wyślesz to zadanko?

maturzysta: Ktoś musi pomóc, bo próbuje uzależnić obwód od samego c, ale ciągle mi zostaje jeszcze jedna niewiadoma. http://s31.postimg.org/nz9zci2dn/WP_20160422_21_26_47_Pro.jpg

maturzysta: refresh//// jak ktoś ma pomysł to poprosiłbym, bo trochę ciekawy jestem tego równania ze zmiennymi....

Eta: Z treści zadania 2x+b=6 ⇒ b= 6−2x , x∊(0,3)

	4−b
y=		= ..... y= x−1 , x>1 i x ∊(0,3) to x ∊(1,3)
	2

h²=x²−y² ⇒ h²= 2x−1

a+b
	=....... = 5−x
2

P²= (5−x)²*(2x−1) P(x)= √(5−x)²(2x−1) dla x ∊(1,3) P^'(x)=....... ........................................................

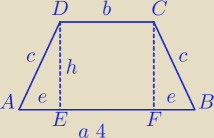
Mila: a+b+2c=10⇔ a+b=10−2c b+2c=6⇔b=6−2c, c>0 i c<3 e=(a−b):2=U{4−6+2c):2= c−1 W ΔAED: c²=h²+e² ⇔c²=h²+(c−1)² c²=h²+c²−2c+1 0=h²−2c+1 h²=2c−1, 2c−1>0 i c>0 h=√2c−1

	a+b
P=		*√2c−1
	2

	10−2c
P(c)=		*√2c−1=(5−c)*p{2c−1)
	2

	2
P'(c)=−√2c−1+(5−c)*
	2√2c−1

	−(2c−1)+5−c		6−3c
P'(c)=		=
	√2c−1		√2c−1

6−3c=0 c=2 6−3c>0⇔2>c dla c=2 funkcja P(c) ma wartość największą. P(2)=(5−2)*p{2*2−1)=3√3

maturzysta: o jakie wy kochane jesteście.... dziękuje wam Idę to przerysować i opracować.

Eta: