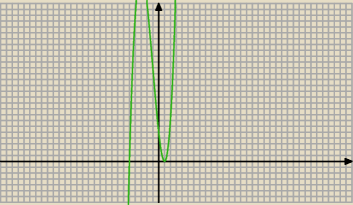
styczne rkwadrat: 1.dla jakiej wartości k wykres wielomianu y=x³+kx−2 jest styczny do osi 0x? 2.wyznacz funkcje postaci f(x)=ax³+bx²+cx+d, która w punktach (1,0) i (−3,32) posiada styczne równoległe do osi 0x. 3.dla każdej z podanych funkcji: f(x)=√3x−2 g(x)=(2x+1)/(2x−1) h(x)=e^x2 rozstrzygnij, czy istnieje styczna do wykresu tej funkcji tworząca z osią 0x: a)kąt ostry b)kąt rozwarty

===: 1) k=−3

rkwadrat: mozesz napisac jak to obliczyłes, albo przynajmniej "punkty" po kolei co mam zrobic?

===: studia czy średnia

Tadeusz: 1) Wynika z tego, że: −funkcja ma ekstremum lokalne w punkcie (a, 0) ... pierwiastek podwójny −a skoro tak to ma trzy pierwiastki Możemy ją zatem zapisać jako f(x)=(x−a)²(x−b)

	2
wiemy, że a2b=2 ⇒ b=
	a2

	2
f(x)=(x−a)2(x−		)
	a2

	2
f(x)=(x2−2ax+a2)(x−		)
	a2

	2		4
f(x)=x3−2ax2+a2x−		x2+		x−2
	a2		a

	2		4
−2a−		=0 a jednocześnie a2+		=k ⇒ k=−3
	a2		a

−2a3−2
	=0
a2

a=−1 Funkcję możemy więc zapisać jako f(x)=(x+1)²(x−2) lub f(x)=x³−3x−2

Tadeusz: f(x)=1x³+3x²−9x+5