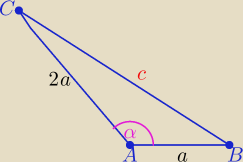
planimetria manny: W trójkącie kąt zawarty między bokami o długościach a i 2a jest rozwarty. Oblicz długość trzeciego boku, wiedząc, że pole trójkąta wynosi ^√3 ₂ a² (w mianowniku jest liczba 2)

Eta: α∊(90^o, 180^o)

	√3a2		1
P(ABC)=		i P(ABC)=		*2a*a*sinα
	2		2

	√3		√3
to a2*sinα=		a2 ⇒ sinα=		⇒ α= 120o (bo trójkąt rozwartokątny)
	2		2

	1
to cos120o= −
	2

z tw. cosinusów c²= 4a²+a²−2*2a*a*cos120^o =........⇒ c=............