STEREOMETRIA Azul: Mógłby ktoś wytłumaczyć? Byłam bym wdzięczna jeśli ktoś krok po korku rozwiązał to zadanie Przekrój osiowy stożka jest trójkątem o obwodzie 24. Jakie wymiary musi mieć ten stożek, aby jego objętość była jak największa?

===: matura "za pasem" ... polski też zdajesz ... więc byłabym a nie byłam bym

Azul: świetnie dziękuję ale pytanie nie dotyczyło mojej ortografii

Metis: Chcesz ze względu na r czy H?

Damian: lepiej od R, zeby pojawił sie pierwiastek

Metis: Niech będzie r Już piszę.

===: Przekrój osiowy to trójkąt równoramienny o danym obwodzie Pitagorasem wyznaczysz H stożka za pomocą podstawy a Poem wzór na objętość stożka Otrzymasz

	1		a2
V=		π		√164−12a
	3		4

dalej pochodna itd

maturzysta: Te zadania na optymalizacje to najłatwiejsza rzecz chyba jaka występuje na maturze, aby tylko na poczatku poprawnie wzór na pole/objetosc napisać i dalej już czysta matma.

Metis: Przekrój osiowy stożka jest trójkątem o obwodzie 24. Jakie wymiary musi mieć ten stożek, aby jego objętość była jak największa? Rozwiązanie Objętość stożka wyraża się wzorem:

	1
V=		πr2*H
	3

Wiemy, że przekrojem osiowym stożka jest trójkąt równoramienny, o równych ramionach l ( tworząca stożka ) i podstawie 2r(średnica). Zatem: 2r+2l=24 2(r+l)=24 r+l=12 l=12−r 12−r>0 r<12 Z twierdzenia Pitagorasa mamy: r²+H²=l² stąd: .H²=(12−r)²+r² H²=144−24r+r²+r² H=√2r²−24r+144

	1		π
Nasze V(r)=		πr2*√2r2−24r+144= V(r)=		√r4(2r2−24r+144)
	3		3

Widzimy, że ta funkcja przyjmie największą wartość wtedy , gdy liczba podpierwiastkowa osiągnie właśnie wartość największą. Nie musimy liczyć pochodnej całej funkcji. Powołujemy się na def. funkcji pierwiastek kwadratowy z...

Metis: Coś mi się nie podoba to co zapisałem

Damian: H²= (12−r) ² − r²

Metis: No właśnie Niech sobie poprawi Wtedy się wszystko zgadza.

Azul: tylko w kluczu jak wyznaczyłam h=√144−24r jest r∊(0;6) i np czy jeśli tego nie napisze: r∊(0;6) to będzie jakiś błąd? Metis w h r² odejmą się i zostanie 0

	2√6
i miałam problem z tym V(r)=		πr2√6−r bo nie wiem co gdzie trzeba wstawić żeby to
	3

uzyskać..

Metis: Nie zostanie 0... Popraw ten zapis V(r) u mnie.

Damian: za brak dziedziny jest −1pkt

Azul: h²=(12−r)²−r²=144+r²−24r+r²=144−24r >>> r²−r²=0

Metis: H²=144−24r+r²−r² =144−24r H=√144−24r Popraw teraz mój zapis V(r)...

Azul: no przecież napisałam to samo co Ty xD ok poprawie

Mila: Liczyć pochodną szanowni maturzyści. Są kłopoty? Azul ma dobry wzór na V , 18:51 0<r<6

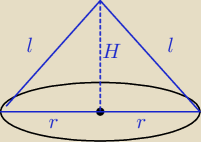
Metis: Przekrój osiowy stożka jest trójkątem o obwodzie 24. Jakie wymiary musi mieć ten stożek, aby jego objętość była jak największa?

	π
V=		r2*H
	3

2r+2l=24 ⇔ r+l=12 ⇔ l=12−r W trójkącie prostokątnym przyprostokątna nie może być dłuższa od przeciwprostokątnej: r<12−r i r>0 , stąd r∊(0,6) H²=l²−r² , podstawiając otrzymane l H=√(12−r )²−r² H=√(12−r−r)(12−r+r) ⇔ H=√12(12−2r) ⇔ H=√24(6−r) ⇔ H=2√6*√6−r

	2√6
V(r)=		πr2*√6−r
	3

Teraz albo V'(r) albo:

	π		π
V(r)=		r2*√24(6−r) =		√24r4(6−r)
	3		3

V(r) przyjmie największa wartość tam gdzie liczba podpierwiastkowa 24r⁴(6−r) . Niech f(r)=24r⁴(6−r) Wtedy: f'(r)=−24r³(5 r−24) Warunek istnienia ekstremów f'(r)=0 , stąd: f'(r)=0 ⇔ −24r³(5 r−24) =0

	24
r=0 v r=
	5

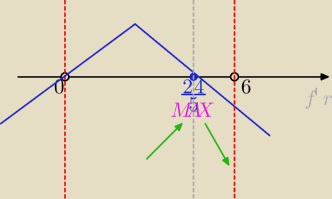
Metis: Ciąg dalszy:

	24
Zatem największą objętość będziemy mieli dla r=		.
	5

Stożek musi mieć następujący wymiary:

	24		12√5		36
r=		, H=		, l=
	5		5		5

Mila:

	2√6π
V(r)=		*r2*√6−r
	3

0<r<6

	2√6π
V'(r)=		*[2r√6−r+r2*U{−1}{2√6−r]=
	3

	2√6π		4r*(6−r)−r2
=		*		=
	3		2√6−r

	2√6π		24r−5r2
=		*
	3		2√6−r

V'(r)=0⇔24r−5r²=0 i 0<r<6

	24
r=
	5

	24
r*(24−5r)>0⇔r∊(0,		)
	5

	24
Dla r=		funkcja V(r) ma wartość największą.
	5

Teraz obliczyc wymiary :h, l

Metis: