Planimetria :( Karol : Z punktu P należącego do boku AB trójkąta równobocznego ABC poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta, jaki tworzy półprosta z odcinkiem AP, jeśli | AP | : | PB |=3 Nie mam kompletnie pojęcia jak się zabrać za to zadanie.

g:

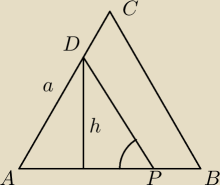
1		3		a2*√3/4		h
	*		a*h =		tg α =
2		4		2		3/8 a

g: Pomyłka! Tam nie jest 3/8 a. Jeszcze pomyślę, albo ktoś inny pociągnie.

g: Oznaczam przez E − punkt przecięcia h z odcinkiem AB. Z Talesa: |AE| / (a/2) = h / (a*√3/2)

	h
tg α =
	3/4 a − |AE|

Karol : dziękuje serdecznie

Eta: Z treści zadania P(APD)= 0,5 P(ABC) , P(ABC)= 4x²√3

	1
to P(APD)= 2x2√3 i P(APD)=		3x*h
	2

	4		h		4
zatem 3xh=4x2√3 ⇒ h=		x√3 oraz		= tg60o ⇒ |AE|=		x
	3		|AE|		3

	5
to |EP|=3x−|AE|=		x
	3

	h		4√3
tgα=		= ....=
	|EP|		5