Znajdź A ∪ B, A ∩ B, A \ B, oraz B \ A dla następujących przedziałów Mati2808: Znajdź A ∪ B, A ∩ B, A \ B, oraz B \ A dla następujących przedziałów: a) A = (−∞, 3> i B = (−2, −7) 2

	2
b) A = (−5, 34) i B = <−1		, 23>
	3

Bardzo proszę o rozwiązanie i wyjaśnienie.

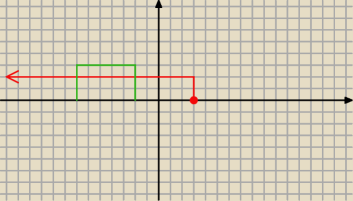
zef: I odczytuj

Mati2808: Niestety nadal nie rozumiem

Mati2808: Czy b bedzie wygladalo tak ?

zef: Tak

zef: Robię A AuB= (−∞;3> AnB=(−7;−2) A\B=(−∞;−7)u(−2;3> B\A=∅

Mati2808: Mogł bys mi jeszcze tylko slownie wytlumaczyc co oznacza u, n, / i \ ? Chodzi o to że np nie wiem co oznacza \ i dlaczego wynosi 0

zef: Ja te swoje "u" i "n" pisałem jako: u=∪− suma (czyli wszystko co mamy na osi) n=∩ − część wspólna (coś co znajduje się w obu zbiorach) \=różnica a\b(a minus b) ∅−to nie jest zero tylko zbiór pusty czyli jeśli b\a=∅ to oznacza że nie ma takiej liczby która należy do zbioru b i nie należy do a

Mati2808: Naprawde dziękuje Ci serdecznie, bardzo mi pomogłeś.

zef: Nie ma sprawy

Mati2808: Kurcze, a mógł bym jeszcze tylko dla pewnosci zobaczyc ile bedzie wynosilo w B) b\a ?

Przemysław: ∅, bo B⊂A ⊂− zawiera, czyli każdy element z B jest w A jak wyrzucisz z B wszystkie, które są w A to nie będzie takiego, który by został.