szereg geometryczny, dwa rozwiązania potencjalna_maturzystka: Dla jakich wartości parametru m równanie 1+x+x²+...=x+m, gdzie lewa strona jest sumą szeregu geomtrycznego, ma dwa rozwiązania? Generalnie to w końcu to rozwiązałam, ale by mi tego prawdopodobnie nie uznali na maturze. W 100% dobrze mam jedynie do momentu, w którym wyznaczyłam m należące do przedziału od (−∞, −3) suma (1, ∞). Błąd pojawia się pewnie dalej. Przekształciłam funkcję tak, by otrzymać równanie: m=(x²−x+1):(1−x) Co dalej powinno się zrobić? Obliczyłam dla prawej strony równania f(−1) i f(1). Dla f(−1) wychodziło m=3/2, a dla f(1)=1/0, więc coś jest źle. W odpowiedzi jest, że m∊(1,3/2) Z czego wynika, że (tak się domyślam) m<f(−1) i m>f(1). Ktoś mi wyjaśni, dlaczego tak i gdzie robię błąd?

ZKS: Skąd ktoś może wiedzieć gdzie robisz błąd skoro podajesz w strzępkach swoje odpowiedzi. Zapisz od początku do końca jak robisz. Zobacz również jak się tutaj zapisuje, abyś otrzymywała ułamki. Kliknij na Kliknij po więcej przykładów używaj dużego U.

Jerzy: Pokaż jak policzyłaś/eś lewą stronę

Jerzy: .... i jakie zrobiłaś/eś załozenia ?

potencjalna_maturzystka:

	1
S=
	1−x

1
	=x+m
1−x

x²−x(1−m)−m+1=0 Δ=m²+2m−3 m1=1 m2=−3 m∊(−∞,−3)U(1,∞) warunek |x|<1, więc x∊(−1,1)

1
	=x+m
1−x

	x2−x+1
m=
	1−x

x∊(−1,1), więc: m<f(−1) (nie wiem, skąd ten warunek ani czy poprawny)

	1+1+1
m<
	1+1

	3
m<
	2

m>f(1) (jak wyżej)

	1
m>... wlasnie tutaj jest coś nie tak, bo mi wychodzi f(1)=
	0

chyba wyszło nie najgorzej z tym formatem

ZKS: Gdzie założenia?

ZKS: Dobra widzę, widzę.

potencjalna_maturzystka: jedyne założenia to |x|<1 i Δ>0

potencjalna_maturzystka: ale nie wiem, skąd to zadanie, bo mi kumpel wysłał. Chyba z Nowej Ery

ZKS: Masz otrzymać dwa rozwiązania w zbiorze x ∊ (−1 ; 1). Niech f(x) = x² − x(1 − m) − m + 1, wtedy Δ ≥ 0 ∧ f(−1) > 0 ∧ f(1) > 0 ∧ −1 < x_w < 1.

potencjalna_maturzystka: Dlaczego Δ≥0, a nie Δ>0? Dla dwóch rozwiązań chyba musi być Δ>0. Z wierzchołkiem rozumiem. Nawet miałam to zapisane na innej stronie, bo coś mi świtało, że coś z tym się robiło, ale już zapomniałam co. I skreśliłam Dlaczego f(1)>o i f(−1)>0? Z tym warunkiem mam największy kłopot.

ZKS: Nie ma słowa o dwóch różnych, dlatego dałem Δ ≥ 0. Narysuj sobie dowolną funkcję kwadratową, gdzie a > 0 i zaobserwuj, dlaczego f(1) > 0 oraz f(−1) > 0. Jak dalej będą problemy postaram się wytłumaczyć.

potencjalna_maturzystka: A no tak, faktycznie. Zawsze może być podwójny pierwiastek. Z f(1)>0 i f(−1)>0 chodzi po prostu o to, że żeby istniał pierwiastek, to wartości muszą być dodatnie? Gdyby były mniejsze od zera, to miejsca zerowe znajdowałyby się "poza" −1 i 1 (dalej), dobrze rozumiem?

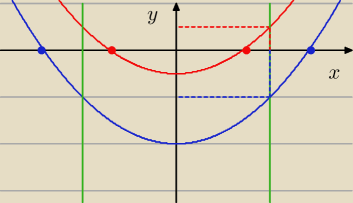
ZKS: Dla niebieskiego wykresu y(1) < 0, co za tym idzie pierwiastek jest poza rozpatrywanym przedziałem, natomiast dla czerwonego wykresu y(1) > 0, więc pierwiastek będzie należał do rozpatrywanego przedziału.

potencjalna_maturzystka: Czyli dobrze rozumiem Może jest dla mnie nadzieja na maturze Dziękuję bardzo!

ZKS: Tylko musisz uważać, bo coś może stać przy najwyższej potędze i trochę inaczej to będzie wyglądać.