..
Michał: Dzień dobry, mam pytanie do tego zadania:
Promień podstawy stożka jest równy 3, a cosinus kąta nachylenia jego tworzącej do podstawy
wynosi 1/3. Oblicz długość krawędzi sześcianu wpisanego w ten stożek (sześcian jest wpisany w
stożek, jeśli cztery jego wierzchołki należą do podstawy stożka, a pozostałe cztery
do powierzchni bocznej stożka).
Obliczyłem tworzącą stożka i wysokość i teraz chce skorzystać z podobieństwa trójkątów, ale w
rozwiązaniu pojawiają się jakieś przekątne
kwadratu, a nie wiem dlaczego. Jak ustawiony jest ten sześcian w stożku w przekroju osiowym?
21 kwi 15:26
Jack: xD
21 kwi 15:29
Jack: przejmuje
21 kwi 15:30
Jerzy:
Musisz nsrysować przekrój płaszczyzną przechodzącą przez przekątną podstawy sześcianu
21 kwi 15:32
Michał: Bez całego rozwiązywania, bo to nie jest jakieś trudne zadanie, tylko ta przekątna mnie
zastanawia bo wydawało mi się że
na przekroju ''patrzymy'' na bok sześcianu a nie na jego przekątną.
21 kwi 15:32
Michał: Ale już chyba widze

21 kwi 15:33
Jerzy:
We widoku będziesz miał prostokąt wpisany w trójkąt
21 kwi 15:37
Jack:
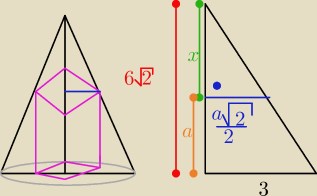
H = 6
√2
x = H − a
ukladamy proporcje z podobienstwa trojkatow...
czyli
H znasz...oblicz a
21 kwi 15:38
Michał: Dziękuje wam bardzo, wszystko już jest jasne.

21 kwi 15:41
Michał: Tak jeszcze wracając do tego zadania, może znać jakieś zadanie w tym stylu żebvym mógł to
jeszcze przetrenować?
21 kwi 16:15

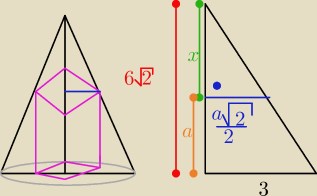 H = 6√2
x = H − a
ukladamy proporcje z podobienstwa trojkatow...
H = 6√2
x = H − a
ukladamy proporcje z podobienstwa trojkatow...
