| 10976sinα*cosα2 | ||
| 3(sinα+1)2*tgβ |

 1 rys.
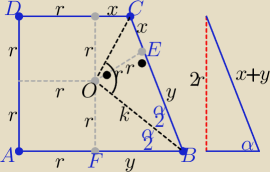
1/ krok rozpatrujemy podstawę, która jest trapezem o podanych warunkach w zadaniu
P= 2r2+r*(x+y) z warunku zadania : 4r+2x+2y=56 ⇒ 2r+(x+y)=28
P= 2r2+r(28−2r) = 28r [j2]
1 rys.
1/ krok rozpatrujemy podstawę, która jest trapezem o podanych warunkach w zadaniu
P= 2r2+r*(x+y) z warunku zadania : 4r+2x+2y=56 ⇒ 2r+(x+y)=28
P= 2r2+r(28−2r) = 28r [j2]
| 2r | 2r | 2r | ||||
i sinα= | ⇒ x+y= | to 2r+ | = 28 |:2 | |||
| x+y | sinα | sinα |
| sinα+1 | 14sinα | |||
zatem r | =14 ⇒ r= | |||
| sinα | 1+sinα |
| 28*14sinα | 392sinα | |||
P= | = | |||
| 1+sinα | 1+sinα |
| r | α | r | 14sinα | |||||||||||||
=sin | ⇒ k= | = | ⇒ | |||||||||||||
| k | 2 |
| (1+sinα)*sinα/2 |
| 14*2sinα/2*cosα/2 | 28*cosα/2 | |||
k= | = | |||
| (1+sinα)sinα/2 | 1+sinα |
| k | k | 28 cosα/2 | ||||
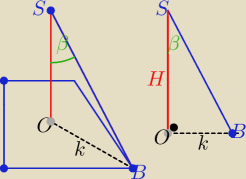
Z trójkąta BOS : | =tgβ ⇒ H= | = | ||||
| H | tgβ | (1+sinα)*tgβ |
| 1 | 392*28sinα*cosα/2 | |||
V= | Pp*H= | = | ||
| 3 | 3(1+sinα)2*tgβ |
| |||||||||||
V= | |||||||||||
| 3(1+sinα)*tgβ |
| |||||||||||
V= | |||||||||||
| 3(1+sinα)2*tgβ |