:)
Metis:
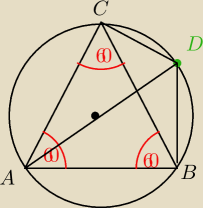
Zadanie dla
Jack
Wykazać, że |CD|+|BD|=|AD|
D − dowolny punkt na okręgu
20 kwi 17:25
ICSP: |AC| = |BC| = |AB| = a > 0
mamy:
|AC| * |BD| + |CD| * |AB| = |AD| * BC|
|BD|*a + |CD| * a = |AD| * a // : a > 0
|CD| + |BD| = |AD|
⬠
20 kwi 17:28
Metis: No nie psuj zabawy!

20 kwi 17:29
Metis: Usuń

20 kwi 17:32
ICSP: NIe mogę

20 kwi 17:38
Jack: 
20 kwi 17:39
Metis: I po ptokach

20 kwi 17:41
Jack: twierdzenie ptolemeusza : DDDDDDDD
20 kwi 17:41
ICSP: 
20 kwi 17:41
Jack: bez znania tego twierdzenia to pewno duzo roboty
20 kwi 17:42
Metis: Właśnie można podobno polem.
20 kwi 17:42
ICSP: 
20 kwi 17:43
 Zadanie dla Jack
Wykazać, że |CD|+|BD|=|AD|
D − dowolny punkt na okręgu
Zadanie dla Jack
Wykazać, że |CD|+|BD|=|AD|
D − dowolny punkt na okręgu






