ostrosłup rafal: Podstawą ostrosłupa ABCDS jest czworokat ABCD. Przekątna AC tego czworokąta ma długość 10√3, a kąt ADC ma miarę 120* stopni. Każda krawędź boczna tego ostrosłupa ma taką samą dlugość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi AS.

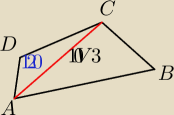
rafal: czy z tw. sinusów jezeli oblicze promień okręgu opisanego na trójkącie ADC to to będzie też promien okręgu opisanego na czworokącie ABCD?

rafal: up

rafal: pomożcie prosze

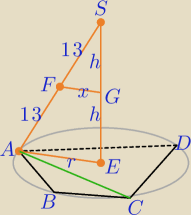
Bogdan: Szkic. Jeśli wszystkie krawędzie ostrosłupa są równe, to spodkiem wysokości jest środek okręgu opisanego na podstawie ostrosłupa.

	1
Trójkąty FGS i AES są pdobne w skali 1:2, stąd x =		r
	2

Oblicz dlugoś promienia r

rafal: Jak obliczyc długosc promienia r ?

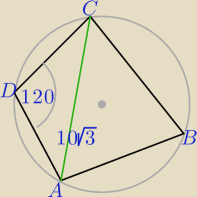
Bogdan: r można obliczyć z twierdzenia sinusów dla trójkąta ACD

rafal: dziekuje