trójkąt opisany na okregu Jolanta: Mam prosbę czy moglibyście spojrzeć na zadanie Gambita ?

Mila: Co chcesz wiedzieć?

Jolanta: Chciałabym wiedzieć jak najprościej zrobić

Jolanta: Zrobiłam to zadanie zaczynajac od tego ze poprowadziłam dwusieczną i policzyłam tg 15⁰ a póżniej 1/2 podstawy

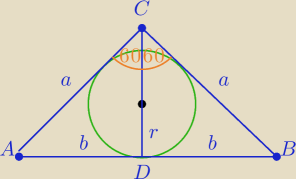
Mila: |AB|=2b

	1		a2*√3
PΔABC=		a2*sin(1200)=
	2		4

	2a+2b
PΔABC=		*r=(a+b)*3
	2

Porównanie pól

	a2*√3
3*(a+b)=		⇔12(a+b)=a2√3
	4

W ΔCDB:

	b
sin(60)=		⇔
	a

	√3
b=a*
	2

==========

	√3
12*(a+a*		)=a2*√3
	2

	√3
12a*(1+		)=a2*√3
	2

6*(2+√3)=a√3 /*√3 6√3*(2+√3)=3a a=2√3*(2+√3)

	√3		√3
2b=2*a*		=2*2√3*(2+√3)*
	2		2

2b=6*(2+√3) Odp: a=2*(2√3+3) |AB|=6*(2+√3)

Jolanta: Milu bardzo Ci dziekuję

Mila:

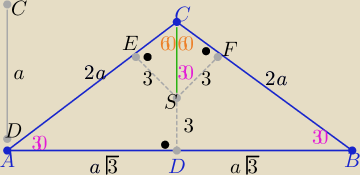
Eta: Podam jeszcze inny sposób Z trójkątów "ekierek" 30^o,60^o, 90^o ΔADC : |AD|=a√3, |CD|= a , |AB|=2a√3 ΔCSF: |SF|= r=3 to |CS|= 2√3 to a= |CD|= r+|CS| ⇒ a= 3+2√3 to: |AB|=2a√3= 2√3*(3+2√3) =12+6√3= 6(2+√3)