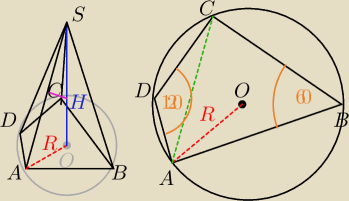
stereometria Metis: Stereometria Podstawa ostrosłupa ABCDS jest czworokąt ABCD. Przekątna AC tego czworokąta ma długość 10√3,a ∡ADC ma miare 120^o.. Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi AS. Rozwiązanie Jeśli wszystkie krawędzie boczne ostrosłupa ABCDS są równe i wynoszą 26 , to ostrosłup jest prosty i spodek wysokości tego ostrosłupa O jest środkiem okręgu opisanego na czworokącie ABCD. Jeśli ∡ADC=120^o , to na podstawie tw. o okręgu opisanym na czworokącie, ∡ABC=180^o−∡ADC = 60^o Okrąg opisany na tym czworokącie jest także okręgiem opisanym na trójkątach ΔACD oraz ΔABC, zatem promień R takiego okręgu wyrazić możemy wzorem( w oparciu o ΔABC):

	|AC|		|AC|
2R=		⇔ 2R=
	sin∡ABC		sin60o

	√3
Wstawiając podane wartości |AC|=10√3 i sin60o=		, otrzymuję:
	2

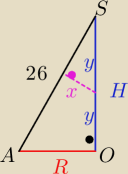
R=10 Na podstawie twierdzenia Pitagorasa w prostokątnym ΔAOS: R²+H²=|AS|², stąd H²=576 i ostatecznie H=24 I teraz mam problem z policzeniem odcinka x.

	1
Na początku miałem pomysł, aby skorzystać z trójkątów podobnych i napisać x2=		H2 , ale
	4

ten odcinek dzieli Nam |AS| na pewne odcinki, a nie H. Nie wiem na co mogę się powołać by obliczyć szukany odcinek.

Metis:

	H
y=
	2

Kacper: Zrobiłeś 90% i zostało tylko podstawić

Metis: Cześć Kacper Do czego podstawić? Nie wiem w jakim stosunku x dzieli |AS|

Metis: Przecież to można z pola...

Metis: H*R / 2=P= 26*x/ 2

Metis: I załatwione

Marchin: Nic nie jest załatwione wyobraź sobie że ten mały trójkąt to element układanki w myślach wyciągasz go i wkładasz ponownie tym razem by pokryły się kąty proste. I potem lecisz z podobieństwa trójkątów.

Metis: ...załatwione

Mila:

x		R
	=
y		26

Metis: Milu polem wychodzi mi inaczej. Wiemy, że pole trójkąta prostokątnego to (R*H)/2 = 120 oraz (|AS|*x)/2=P , więc

	120
13x=120 , x=
	13

Z twojej proporcji: x/12= 10/26 26x=120 ....

Marchin: x to nie jest wysokość w trójkącie AOS

Mila: Właśnie.

Metis: Racja, nie zauwazyłem − przecież nie wychodzi z wierzchołka... Dziękuje

Mila: