zadania optymalizacyjne rkwadrat: zadania optymalizacyjne 1. Trzy boki czworokąta mają długość 1 cm. Jaka powinna być długość czwartego boku i jaki powinien być kształt czworokąta, żeby , aby jego pole było największe możliwe? 2. W półkole o promieniu R wpisać prostokąt o największym polu, którego dwa wierzchołki leżą na półokręgu i dwa na średnicy.

rkwadrat: ktos cos?

rkwadrat: proszeee

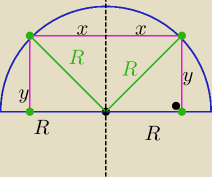
Jack: założenia : x,y,R > 0 2x<2R −>> x<R y<R z Pitagorasa: R² = x² + y² y = √R²−x² −>>kolejne założenie (R² − x² ≥ 0 −>>stąd x∊<−R;R>) Pole prostokata = P = 2x * y = 2x * √R²−x² = √4x²(R²−x²) = √4x²R² − 4x⁴ pole maxymalne funkcji f(x) = 4x²R² − 4x⁴ bedzie dla tego samego argumentu co dla P f(x) = 4x²R² − 4x⁴ f ' (x) = 8xR² − 16x³ 8xR² − 16x³ = 0 /// : 8 xR² − 2x³ = 0 x(R² − 2x²) = 0 x = 0 lub R² = 2x²

	R2
x = 0 lub x = √
	2

rysujemy krzywa, przedzialy monotonicznosci, itd

	R2
widzimy ze f max dla x = √
	2

zatem

	R2		R2
Pole max = √4x2(R2−x2) =√4*		(R2−		) =
	2		2

	R2
= √2R2(R2−		) = √2R4 − R4 = √R4 = R2
	2

rkwadrat: dziekuje

rkwadrat: a 1 zad

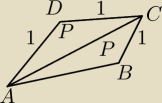
Damian: P_c= P_ABC + P_ACD P = 1/2 * a *b*sin(kata miedzy a i b) sin_max dla kata 90 = 1 wiec jest to kwadrat o boku 1

jc: Damian, a co powiesz o trapezie o bokach 2, 1, 1, 1 ?

Damian: że niestety Pole ma > 1.

jc: Myślę, że opisany trapez ma najwększe pole = 3√3/4. Jak to pokazać? Może trzeba spojrzeć na sześciokąty o bokach = 1?