asd olekturbo: Kąt nachylenia ściany bocznej ostrosłupa parwidłowego trójkątnego do płaszczyzny podstawy jest alfa. Krawedz boczna jest a. Wyznacz objetosc. Bylby ktos chetny policzyc? Nie wiem czy dobrze mi wyszlo

	a3tga√3
V =
	4(tg2a+1)(√tg2a+1)

Iryt: Doprowadź do prostszej postaci :

	sin2α+cos2α		1
tgα+1=		=
	cos2α		cos2α

Zaraz rozwiążę.

olekturbo: dzieki

olekturbo: Ogolnie wyszedlem z tego, ze

	2
x =		h
	3

x²+H² = a²

H
	= tga
x

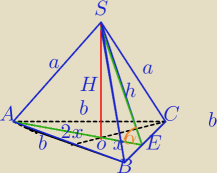
Iryt: Tak zaznaczyłeś kąt?

olekturbo: tak

Iryt: Mam takie obliczenia: b− krawędź podstawy a²=H²+(2x)² |OE|=x

	H
tgα=
	x

H=x*tgα a²=(xtgα)²+4x² a²=x²tg²α+4x² a²=x²*(tg²α+4)

	a2
x2=
	tg2α+4

	a
x=
	√tg2α+4

	1
b2=(3x)2+(		b)2
	2

Licz dalej sam. Nieznaczne będą różnice, metodę dobrą obrałeś.

olekturbo: dzieki