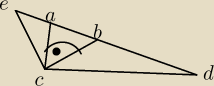
trójkąt Lucas: Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C i obwodzie równym 20 cm. Na prostej AB wybrano punkty D i E leżące na zewnątrz odcinka AB takie, że |AD| = |AC| i |BE| = |BC| (zobacz rysunek obok). Oblicz pole koła opisanego na trójkącie ECD |∡CAD| = 180–α

	180−(180−α)		α
|∡ACD| =		=
	2		2

	β
analogicznie w |∡BCE| =
	2

i tutaj się zaciąłem

	β		α		α+β
|∡ECD| = 90 +		+		= 90+
	2		2		2

da to się policzyć?

Eta:

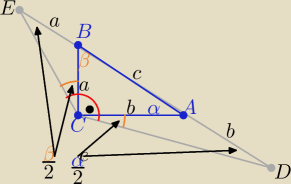
	α		β
|ED|=a+b+c=20 i α+β=90o ⇒		+		=45o
	2		2

	√2
to |∡DCE|= 90o+45o=135o sin135o= sin45o=
	2

z twierdzenia sinusów w trójkącie DCE

|ED|
	= 2R ⇒ R= ..... i Pk= πR2=....
sn135o

dokończ obliczenia

Lucas: dzięki wielkie teraz jest to takie oczywiste

Eta: