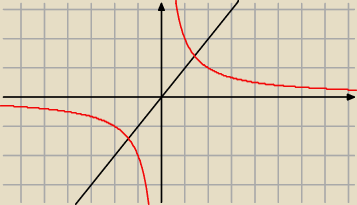
wykresy wymierne 5-latek : Cwiczenie nr 17 gdzie wykres funkcji f_a(a>0 przecina prosta y=x Znajdz funkcje odwrotna do f_a

	2
Zrobilem wykres f2=
	x

czyli przeciana 1 i 3 ćwiartce

	a
f(x)=		i x≠0
	x

	a
y=
	x

	a
y*x=a ⇒ x=
	y

Jerzy:

	a
x =		⇔ x2 = a
	x

5-latek : czesc \Dlaczego tak ?

	a
Wyznaczylem x ze wzoryu y=
	x

Jerzy: Szukasz pumktòw wspólnych dwóch funkcji f(x) = g(x)

5-latek : Przepraszam ale nie rozumiem Cie w tej chwili Być moz epowiniem zrezygnować z tego zadania dzisiaj

	y−1
ale wezmy np. y=2x−1 to y−1=2x to x=		i to jest funkcja odwrotna do danej
	2

5-latek : Mowilem ma być y+1

Jerzy: Co to jest f_a ?

5-latek :

	a
Jest to ogolna posatc funkcji fa(x)=		gdzie za a wstawiam jakas liczbe
	x

	2
czyli np. f2(x)=
	x

5-latek : Wiec co zrobilem zle przy tej funkcji odwrotnej ?

Mila:

	1
1) y=
	x

Prosta y=x Punkty przecięcia:

	1
x=		⇔x2=1 ⇔x=1 lub x=−1
	x

A=(1,1) B=(−1,−1) punkty symetryczne względem O=(0,0) 2)

	4
y=
	x

i y=x

	4
x=
	x

x²=4⇔x=2 lub x=−2 Punkty przecięcia: (2,2) (−2,−2) 3) funkcje odwrotne Prosta y=x jest osią symetrii tych funkcji.

	1		1
f(x)=		to f−1(x)=g(x)=
	x		x

	1
f(g(x))=		=x
	1x

5-latek : Dziekuje . Dopiero teraz jakos funkcjonuje i mysle . Jeszcze jak wieczorem wroce z pracy dopytam o ta funkcje odwrotna

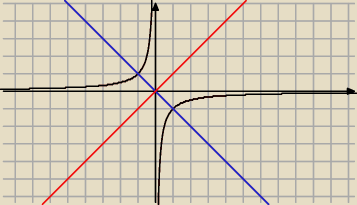5-latek : czyli chodzilo o to z e przecina symetrycznie względem srodka układu wspolrzednych Natomiast dla a<0 bedzie przecinac symetrycznie względem srodka układu wspolrzednych ale prosta y=−x natomiast prosta y=x nie przecina

	a
Wynika to z tego z eproste y=x i y=−x sa osiami symetrii hiperboli równoosiowej f(x)=
	x

5-latek :