optymalizacja, prostokąt o największym polu
Gosia:
Witam! Utknęłam w zadaniu i będę bardzo wdzięczna za pomoc.
Treść brzmi:
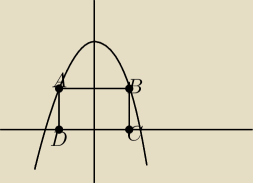
Rozważmy wszystkie prostokąty których dwa wierzchołki należą do paraboli y=−x
2+12, a pozostałe
leżą na osi OX.
Wyznacz wymiary tego z prostokątów, który ma największe pole. Oblicz to pole.
Zaczęłam od wyznaczenia długości odcinków |BC| i |CD|. Odpowiednio:
|BC|=
√(x2−12)=x
2−12
|CD|=
√(2x)2)=2x
P(x)=2x*(x
2−12)=2x
3−24x
Chciałam wyznaczyć teraz pochodną i próbować dalej kombinować (dopiero uczę się rozwiązywać
zadania optymalizacyjne), lecz zajrzałam do odpowiedzi, w których pole wynosi −2x
3+24x.
Nie widzę błędu, a musiałam gdzieś pomieszać się w znakach... Będę wdzięczna za pomoc

 Witam! Utknęłam w zadaniu i będę bardzo wdzięczna za pomoc.
Treść brzmi:
Rozważmy wszystkie prostokąty których dwa wierzchołki należą do paraboli y=−x2+12, a pozostałe
leżą na osi OX.
Wyznacz wymiary tego z prostokątów, który ma największe pole. Oblicz to pole.
Zaczęłam od wyznaczenia długości odcinków |BC| i |CD|. Odpowiednio:
|BC|=√(x2−12)=x2−12
|CD|=√(2x)2)=2x
P(x)=2x*(x2−12)=2x3−24x
Chciałam wyznaczyć teraz pochodną i próbować dalej kombinować (dopiero uczę się rozwiązywać
zadania optymalizacyjne), lecz zajrzałam do odpowiedzi, w których pole wynosi −2x3+24x.
Nie widzę błędu, a musiałam gdzieś pomieszać się w znakach... Będę wdzięczna za pomoc
Witam! Utknęłam w zadaniu i będę bardzo wdzięczna za pomoc.
Treść brzmi:
Rozważmy wszystkie prostokąty których dwa wierzchołki należą do paraboli y=−x2+12, a pozostałe
leżą na osi OX.
Wyznacz wymiary tego z prostokątów, który ma największe pole. Oblicz to pole.
Zaczęłam od wyznaczenia długości odcinków |BC| i |CD|. Odpowiednio:
|BC|=√(x2−12)=x2−12
|CD|=√(2x)2)=2x
P(x)=2x*(x2−12)=2x3−24x
Chciałam wyznaczyć teraz pochodną i próbować dalej kombinować (dopiero uczę się rozwiązywać
zadania optymalizacyjne), lecz zajrzałam do odpowiedzi, w których pole wynosi −2x3+24x.
Nie widzę błędu, a musiałam gdzieś pomieszać się w znakach... Będę wdzięczna za pomoc 