zadanie Metis: Wykaż, że jeśli wielomian H(x) dzieli się przez (x−4)³ to wielomian H'(x) dzieli się przez (x−4)². H(x)=(x−4)³P(x), zatem H'(x)=3(x−4)²P(x)+(x−4)³P'(x) ⇔ (x−4)²[3P(x)+(x−4)P'(x)], zatem H'(x) dzieli się przez (x−4)². Tyle?

ZKS: .

Metis: Dzięki

Metis: ZKS jesteś jeszcze ?

5-latek : Metis na gorze masz te dwa linki

ZKS: Jestem, jestem.

Metis: Zerkniesz? http://i.imgur.com/6Rm8JDE.png Nie przepisuję bo to najnowsza matura zadania.info i nie chcę publikować odpowiedzi

ZKS: Jasne, zaraz spojrzę.

olekturbo: @Metis Matura z matematyki jest 5 czy 6 maja? Na stronie CKE jest napisane, ze 5, a na prawie wszystkich innych, ze 6

olekturbo: I jak tak fajnie sobie wydrukowales to? Bo jak wchodze na zadania.info to mam tylko taka wersje do przegladania on−line

Metis: 5

Metis: Nie potrafię się uczyć z ekranu

olekturbo: Ale jest taki arkusz gotowy do wydruku?

olekturbo: http://www.zadania.info/n/7355335 Bo tu jest np. 6 maja

ZKS: Jest , ale jeszcze musisz dokończyć. To równanie można zapisać równoważnie

	1
cos(4x) = −		.
	2

Metis: Tak, jeszcze przedział Olek > http://www.zadania.info/n/4229016 , stąd można pobrać w takim widoku jakim mam ja.

olekturbo: Dzieki

ZKS: Jak nigdzie nic nie pomyliłem to powinieneś dostać cztery rozwiązania.

Mila: Witajcie, ja mam równoważne:

	1
cos2(2x)=
	4

	11π		5π		4π		7π
x∊{−		,−		,−		,−		}
	6		3		3		6

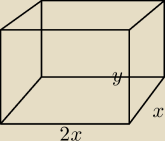
Metis: Milu czy mogłabyś zerknąc za zadanie 16 tej matury ? Moje rozwiązanie: V=2x*x*y, gdzie y to krawędź boczna, a 2x i x wymiary podstawy Wiemy, że P_c=1 Stąd: 2*2x*x+2*2xy+2*x*y−1 4x²+6xy=1 − z tego y 6xy=1−4x²

	1−4x2
y=
	6x

Podstawiam do wzoru na objętość otrzymuję:

	1−4x2		−4x3+x
V(x)=2x2*		=
	6x		3

Szukam maksimum:

	1
V'(x)=−4x2+		− funkcja kwadratowa z ramionami do dołu , zatem osiągnie maksimum.
	3

I wychodzi, że dla x=0 mamy maksimum A x>0

Metis:

Mila: 1) Założenie dla y: 1−4x²>0 2) Nie badasz ekstremów V'(x) lecz V(x) 3) Badasz miejsca zerowe V'(x) , tam mogą być ekstrema. V'(x)=0 i badasz jak zmienia się znak pochodnej przy przejściu przez miejsca zerowe, wtedy określasz jakie jest to ekstremum i czy w ogóle jest.

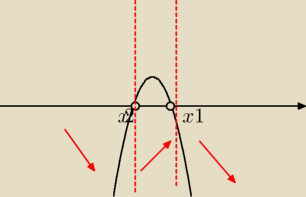
Metis: Hmmm wydawało mi się że y może być dowolnie mały lub dowolnie duży Skąd takie założenie? Nie wiem jak to popsułem

	−4x3+x
V(x)=
	3

	1
V'(x)=−4x2+
	3

Zerowanie się pochodnej to warunek konieczny istnienia ekstremum.

	1
V'(x)=0 ⇔ −4x2+		=0
	3

stąd:

	1		1
x1=		v x2=−
	2√3		2√3

	√3		√3
x1=		v x2=−
	6		6

	√3
Mamy maksimum dla x=
	6

	2√3
y=
	9

Sprawdziłem dla pola i zgadza się

Mila: Wysokość musi być wartością dodatnią.

Metis: Jasne

	1−4x2
y=
	6x

	1−4x2
y>0 ⇔		>0 , x>0
	6x

więc 1−4x²>0

Metis: Dziękuje

Mila: