prosta, trójkąt, długość odcinka mikołaj.L: Dany jest trójkąt, którego wierzchołki mają następujące współrzędne: A(−6,−2), B(10,6) oraz C(3,10). Punkt S to środek odcinka AB. Przez punkt S poprowadzono prostą prostopadłą do odcinka AB. Prosta przecięła bok AC w punkcie P. Oblicz długość odcinka PC.

5-latek : czy brakuje teorii ,czy nie chce się liczyc ? Zrob rysunek do zadania i zobaczysz co masz robic

mikołaj.L: mam zrobione połowę zadania, tylko nie wiem co dalej

mikołaj.L: policzyłem długość AB, wyszło 8 pierwiastków z 5, a więc |AS| = |BS| = 4 pierwiastki z 5

mikołaj.L: policzyłem również długość boku AC, wyszło 15

mikołaj.L: wyliczyłem tez współrzędne punktu S = (2;2)

mikołaj.L: i nie wiem co teraz

mikołaj.L: bardzo proszę o pomoc!

5-latek : Czekaj pomoge

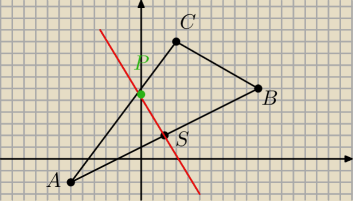
5-latek : Widzisz teraz jak ważne jest poswiecenie 5 minut czasu na zrobienie rysunku (szkicu do zadania WIdzisz teraz ze niepotrzebnie liczyles te dlugosci (one nie sa do niczego potrzebnee 1 Wyznaczylews punt S=(2,2) i Teraz żeby wyznaczyć równanie prostej prostopadlej tej czerwonej to potrzebny jest wspolczynnik kierunkowy prostej AB

	y2−y1
wiec albo liczysz go z ewzoru tgα=a=
	x2−x1

Albo piszsesz równanie prostej przechodzącej przez punkty A I B i wmasz ten wspolczynnik a Potem wiemy ze aby proste były prostopadle a*a₁=−1 POlicz najpierw to co napisałem

mikołaj.L: a więc współczynnik kierunkowy prostej PS równy jest −2

mikołaj.L: bo współczynnik kierunkowy pr. AB wyszedł mi 1/2

5-latek : Masz wspolczynnik kierunkowy tej prostei i punkt S=(2,2) to możesz wyznaczyć równanie prostej PS (wyznacz je)

5-latek : jeśli masz dany wspolczynnik ierunkowy i dany punkt to równanie prostej przechodzzacej przez ten punkt ma postac y=a(x−x₀)+y₀ gdzie x₀ i y₀ to wspolrzedne punktu

mikołaj.L: rowanie pr. PS: y = −2x + 2

mikołaj.L: czy moge teraz policzyć współrzędne punktu P ?

mikołaj.L: wykorzystałbym do tego równanie prostej przechodzącej przez 2 punkty. Czy tak?

5-latek : sprawdze sobie y=−2(x−2)+2 = −2x+4+2= −2x+6 =========== czyli sobie popraw Teraz patrz na rysunek masz równanie prostej PS i musimy wyznaczyć wspolrzedne punktu P Co nam brakuje ? Brakuje równania prostej AC czyli prostej przechodzącej przez punty A i C 1. Piszsez to równanie tej prostej 2. Przyrównujesz do siebie równania prostych AC i PS i wyznaczasz wspolrzena x−owa punktu P 3 Albo do równania prostej PS albo AC wstwiasz to wspolrzedna x_owa i wyliczasz wspolrzedna y_owa punktu P (masz już punkt P $. ZE wzoru na dlugosc odcinka liczysz dlugosc odcinka PC

mikołaj.L: poprawione, faktycznie, pomyliłem się dobrze, już robię dalej

5-latek : Najlepiej pisz tutaj obliczenia .

mikołaj.L: jasne, dziękuję

mikołaj.L: a zatem mam tak: policzyłem wspołczynnik kierunkowy pr. AC: a = 4/3 i teraz prosta AC przechodząca przez punkt P ma postać: y = −2x − 2x₀ + y₀ i teraz przyrównuję: −2x − 2x₀ + y₀ = −2x+6

mikołaj.L: nie, nie, prosta AC przechodząca przez punkt P ma postać

mikołaj.L: y = −4/3 x − 4/3x₀ + y₀

mikołaj.L: *y = −4/3 x + 4/3x₀ + y₀

5-latek : Zle to robisz Masz wyznaczyć równanie prostej AC czyli prostej przechodzącej przez punkty A i C (cale równanie postaci y=ax+b

5-latek : Wspolrzedne punktu P dopiero wyznaczymy

mikołaj.L: aaa, już, dobrze, poprawiam

5-latek : Żeby wyznaczyć punkt przecięcia się prostych musisz mieć ich równania . Nie wystarczy sam wspolczynnik kierunkowy

mikołaj.L: y = 4/3 x + 6

mikołaj.L: rozumiem czyli teraz 4/3 x + 6 = −2x+6, tak?

5-latek : No dobrze No to teraz liczymy

4
	x+6= −2x+6 wyznacz z tego x
3

mikołaj.L: no to x = 0...

mikołaj.L: 4/3x +6= −2x+6 4/3x + 2x = 0 10/3 x = 0

5-latek : To się liczy szybko w pamięci (za długo liczysz

mikołaj.L: czyli x z tego to zero

5-latek : Teraz np. do rownnia prostej AC wstaw x i wylicz y

mikołaj.L: Dobra, to mam współrzędne P −−−> P(0,6) i teraz mogę policzyć długość odcinka PC

5-latek : Tak możesz teraz policzyć dlugosc tego odcinka PC

mikołaj.L: |PC| = 5

5-latek : I taka jest odpowiedz w książce ?

mikołaj.L: Tak

mikołaj.L: DZIĘKUJĘ SERDECZNIE ZA POMOC I POŚWIĘCENIE MI CZASU! i jednocześnie bardzo przepraszam

5-latek : Podstawiaj do wzoru na dlugosc odcinka i licz Za szybko to policzyles w stosunku do tamtych obliczen

5-latek : Na zdrowie