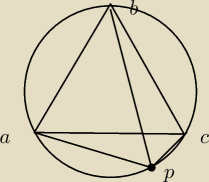
wykaż że szarlotka: Dany jest trójkąt równoboczny ABC wpisany w okrąg. Punkt P leży na krótszym łuku AC. Wykaż, że PB = PA + PC Proszę o pomoc, jestem beznadziejna w wykazywaniu .

Tadeusz: Zauważ, że: ∡APB jak i ∡BPC mają po 60^o Teraz dwukrotnie twierdzenie cosinusów i otrzymasz: |AP|²+|BP|²−|AP|*|BP|=|BP|²+|CP|²−|BP|*|CP| |AP|²−|CP|²+|BP|*|CP|−|AP|*|BP|=0 (|AP|−|CP|)*(|AP|+|CP|)+|BP|(|CP|−|AP|)=0 (|AP|−|CP|)(|AP|+|CP|−|BP|)=0 dalej sama

szarlotka: nie widze tego ze maja po 60

===: jako kąty wpisane oparte na tym samym łuku co kąty trójkąta ( a te mają 60^o