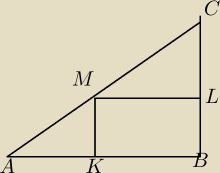
W trojkat prostokatny ABC o przeciwprostokatnej AC wpisao prostokat KBLM. Udowodnij że
| BL | BK | ||
+ | =1 | ||
| BC | BA |
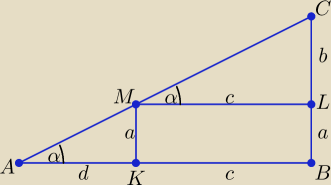Trzeba wyjść od podobieństwa trójkątów: AKM i MLC
| a | b | ||
= | |||
| d | c |
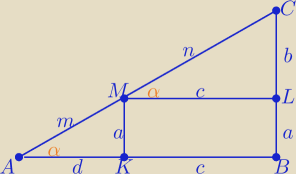Z podobieństwa trójkątów
AKM i ABC i MLC i ABC
| a | m | c | n | ||||
= | i | = | |||||
| a+b | m+n | c+d | m+n |
| |BL| | m | |||
= | ||||
| |BC| | m+n |
| |BK| | n | |||
= | ||||
| |BA| | m+n |
| |BL| | |BK| | m+n | ||||
+ | = | = 1 | ||||
| |BC| | |BA| | m+n |
