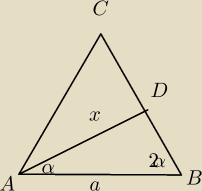
Wykaż że Kiwi: W trójkącie równoramiennym ABC o podstawie AB, gdzie |AB| = a oraz |AC| = |BC| = b,

	√2a2+b2
poprowadzono środkową AD długości x. Wykaż, że x=		.
	2

Próbowałam rozwiązać z zależności kątów ale to mi nic chyba nie dało, z Pitagorasa wyznaczyłam x w dwóch trójkątach, ale jest i tak za dużo danych. Nie mam już pomysłów. Pomoże mi ktoś?

Rafal44: Znasz twierdzenie cosinusów? https://pl.wikipedia.org/wiki/Twierdzenie_Stewarta

Rafal44:

	1   a 2		a
cos(2α)=		=
	b		2b

	1		1		b2		a
x2=a2+(		b)2−2*a*		b*cos(2α)=a2+		−ab*		=
	2		2		4		2b

	b2		a2		a2		b2		1
a2+		−		=		+		=		*(2a2+b2)
	4		2		2		4		4

	1
x=		√2a2+b2
	2

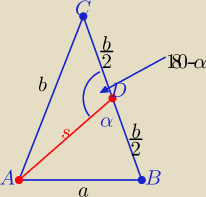Eta: cos(180⁻α)= −cosα dwa razy z tw. kosinusów w trójkątach ABD i ADC

	b2		b
a2=s2+		−2*s		*cosα
	4		2

	b2		b
i b2=s2+		+2*s*		*cosα
	4		2

+ −−−−−−−−−−−−−−−−−−−−−−

	b2		√2a2+b2
a2+b2=2s2+		/*2 ⇒ 4s2= 2a2+b2 ⇒ s=
	2		2

Kiwi: Zaczęłam rozwiązywać wg tw cosinusów ale machnęłam się w znakach. Dzięki za pomoc

Rafal44: Rozwiązanie z zastosowaniem twierdzenia Pitagorasa Niech P będzie takim punktem leżącym na prostej AB, że kąt APD ma miarę 90. Środkowa AD to przeciwprostokątna trójkąta prostokątnego APD. H − spodek wysokości opuszczonej na bok AB z wierzchołka C h − długość tej wysokości

	1
Z podobieństwa trójkątów BPD i BHC w skali 1:2 (cecha kąt−kąt−kąt) |PD|=		h oraz
	2

	1		1		1		1		3
|BP|=		|BH|=		*		a=		a⇒|AP|=		a
	2		2		2		4		4

Na mocy twierdzenia Pitagorasa w trójkącie HBC

	1
h2+(		a)2=b2
	2

	1
h2=b2−		a2
	4

W myśl twierdzenia Pitagorasa w trójkącie APD

	3		1
(		a)2+(		h)2=x2
	4		2

9		1
	a2+		h2=x2
16		4

9		1		1
	a2+		(b2−		a2)=x2
16		4		4

9		1		1
	a2+		b2−		a2=x2
16		4		16

8		1
	a2+		b2=x2
16		4

1		1
	a2+		b2=x2
2		4

1
	(2a2+b2)=x2
4

	1
x=		√2a2+b2
	2