stereometria, przekroje ostrosłupów ania: Podstawą ostrosłupa jest trójkąt prostokątny równoramienny. Wysokość ostrosłupa jest trzy razy dłuższa od przyprostokątnej trójkąta w podstawie, a spodek wysokości jest wierzchołkiem kąta prostego trójkąta w podstawie. Przekrój ostrosłupa płaszczyzną przechodzącą przez przeciwprostokątną podstawy i wysokość ostrosłupa jest nachylony do płaszczyzny podstawy pod kątem α takim , że tgα=√2 wiedząc, że pole przekroju jest równe 8√3, oblicz objętość tego ostrosłupa.

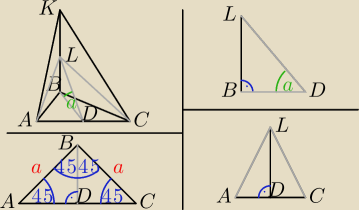
yht: z ΔABC: AC = a*√2

	1
AD =		AC
	2

	1		a*√2
AD =		a*√2 =
	2		2

	BD
tg450 =
	AD

	BD		a*√2
1 =		{2} → BD =
	a*√2		2

z ΔBDL:

	BL
tg(a) =
	BD

	BL		a*√2
√2 =		|*
	a*√2   2		2

	a*√2
√2*		= BL → BL = a
	2

BL²+BD² = DL²

	a*√2
a2 + (		)2 = DL2
	2

	2a2
a2 +		= DL2
	4

	a2
a2 +		= DL2
	2

3a2
	= DL2
2

	√3
DL =		a
	√2

z ΔALC:

	1		a*√2
DC =		AC → DC =
	2		2

P_ALC = 8√3

1
	*AC*DL = 8√3
2

1		√3
	*a*√2*		a = 8√3
2		√2

a2*√3
	= 8√3 |*2
2

a²*√3 = 16√3 |:√3 a² = 16 a = 4 KB = 3*AB → KB = 3a → KB = 12

	1
V =		Pp*h
	3

	1
V =		*PΔABC*KB
	3

	1		1
V =		*		*AB*BC*KB
	3		2

	1		1
V =		*		*a*a*3a
	3		2

	1		1
V =		*		*4*4*12
	3		2

V = 32

ania: dziękuję